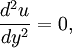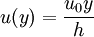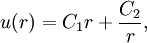My watch list

Couette flow

In fluid dynamics, Couette flow refers to the laminar flow of a viscous liquid in the space between two surfaces, one of which is moving relative to the other. The flow is driven by virtue of viscous drag force acting on the fluid. This type of flow is named in honor of Maurice Marie Alfred Couette, a Professor of Physics at the French university of Angers in the late 19th century.

Additional recommended knowledge

Weighing the right way

Daily Sensitivity Test

Daily Visual Balance Check

1 Simple Conceptual Configuration
- 1.1 Mathematical Description
- 1.2 Constant Shear
2 Taylor's Idealized Model
3 Finite-Width Model
4 Wendl's Result for Physical Devices
5 References
6 See also

Simple Conceptual Configuration

Mathematical Description

Couette flow is frequently used in undergraduate physics and engineering courses to illustrate shear-driven fluid motion^[1]. The simplest conceptual configuration finds two infinite, parallel plates separated by a distance h. One plate, say the top one, translates with a constant velocity u₀ in its own plane. Neglecting pressure gradients, the Navier-Stokes equations simplify to

$\frac{d^2 u}{d y^2} = 0,$

where y is a spatial coordinate normal to the plates and u (y) is the velocity distribution. This equation reflects the assumption that the flow is uni-directional. That is, only one of the three velocity components $(u, v, w)$ is non-trivial. If y originates at the lower plate, the boundary conditions are u(0) = 0 and u(h) = u₀. The exact solution

$u (y) = \frac{u_0 y}{h}$

can be found by integrating twice and solving for the constants.

Constant Shear

A notable aspect of this model is that shear stress is constant throughout the flow domain. In particular, the first derivative of the velocity, u₀ / h, is constant. (This is implied by the straight-line profile in the figure.) According to Newton's Law of Viscosity (Newtonian fluid), the shear stress is the product of this expression and the (constant) fluid viscosity.

Taylor's Idealized Model

The configuration shown in the figure cannot actually be realized, as the two plates cannot extend infinitely in the flow direction. Sir Geoffrey Taylor was interested in shear-driven flows created by rotating co-axial cylinders. He reported a mathematical result in 1923 that accounts for curvature in the flow direction having the form^[2]

$u (r) = C_1 r + \frac{C_2}{r} ,$

where C₁ and C₂ are constants that depend on the rotation rates of the cylinders. (Note that r has replaced y in this result to reflect cylindrical rather than rectangular coordinates.) It is clear from this equation that curvature effects no longer allow for constant shear in the flow domain, as shown above. This model is incomplete in that it does not account for near-wall effects in finite-width cylinders, although it is a reasonable approximation if the width is large compared to the space between the cylinders. Generalizations of Taylor's basic model have also been examined. For example, the solution for the time-dependent "start-up" process can be expressed in terms of Bessel functions^[3].

Finite-Width Model

Taylor's solution accounts for the curvature inherent in the cylindrical devices typically used to create Couette flows, but not the finite nature of the width. A complimentary idealization accounts for finiteness, but not curvature. In the figure above, we might think of the "boundary plate" and the "moving plate" as the edges of two cylinders having large radii, say $R 1$ and $R 2$ , respectively, where $R 2$ is only slightly greater than $R 1$ . In this case, curvature can be neglected locally. The physicist/mathematician Ratip Berker reported a mathematical solution for this configuration in terms of a trigonometric expansion^[4]

Wendl's Result for Physical Devices

Actual co-axial cylinder devices used to create Couette flows have both curvature and finite geometry. The latter gives rise to increased drag in the wall region. A mathematical result that accounts for both of these aspects was given only recently by Michael Wendl^[5]. His solution takes the form of an expansion of modified (hyperbolic) Bessel functions of the first kind.

References

^ B.R. Munson, D.F. Young, and T.H. Okiishi (2002) Fundamentals of Fluid Mechanics, John Wiley and Sons. ISBN 0-471-44250-X.
^ G.I. Taylor (1923) Stability of a Viscous Liquid Contained between Two Rotating Cylinders, Philosophical Transactions of the Royal Society of London. Series A 223, 289-343.
^ C.J. Tranter (1968) Bessel Functions with Some Physical Applications, The English Universities Press. (see pp. 115-116).
^ R. Berker (1963) Intégration des équations du mouvement d'un fluide visqueux incompressible, in Handbuch der Physik 8(2), S Flügge (ed.), Springer-Verlag.
^ M.C. Wendl (1999) General Solution for the Couette Flow Profile, Physical Review E 60, 6192-6194.