To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Reynolds transport theorem
Reynolds transport theorem is a fundamental theorem used in formulating the basic conservation laws of fluid dynamics. These conservation laws (law of conservation of mass, law of conservation of linear momentum, and law of conservation of energy) are adopted from classical mechanics and thermodynamics where the system approach is normally followed. In fluid mechanics, it is often more convenient to work with control volumes as it is difficult to identify and follow a system of fluid particles. Thus, there is a need to relate the system equations and corresponding control volume equations. The link between the two equations is given by the Reynolds Transport Theorem. Imagine a system and a coinciding control volume with a control surface. Reynolds transport theorem states that the rate of change of an extensive property N, for the system is equal to the time rate of change of N within the control volume and the net rate of flux of the property N through the control surface. For an example, the law of conservation of mass states that rate of change of the property, mass, is equal to the sum of the rate of accumulation of mass within a control volume and the net rate of flow of mass across the control surface. The differential forms of these equations with additional assumptions are commonly known as the Navier-Stokes equations. The additional assumptions are the Newton's viscosity law and the Fourier's conduction law. Product highlight
General FormThe Reynolds transport theorem refers to any extensive property, N, of the fluid in a particular control volume. It is expressed in terms of a substantive derivative on the left-hand side.
where η is N per unit mass, t is time, c.v. refers to the control volume, c.s. refers to the control surface, ρ is the fluid density, V is the volume, υb is the velocity of the boundary of the control volume (the control surface), υr is the velocity of the fluid with respect to the control surface, n is the outward pointing normal vector on the control surface, and A is the area. Mass FormulationAlso called the continuity equation, the control volume form of the conservation of mass is found by substituting mass in for N. This means that η is equal to 1.
All variables are defined as in the general formulation. M is equal to the mass of the control volume. Applying the Conservation of mass principle, the left hand side reduces to 0 since mass of a system cannot change in time. In a steady flow system, the first term on the right hand side of the equation will be equal to 0, i.e. the mass of the control volume does not change, implying that the mass flow rate into the control volume is equal to the mass flow rate out of the control volume. Momentum FormulationThe momentum equation is found by substituting momentum in for N. From this, η is found to be velocity. The time rate of change of momentum (now the left hand side of the equation) is, from Newton's second law, equal to the net force. Note that this is a vector equation.
where F is force, υ is the velocity of fluid in a coordinate system attached to the control surface, and all other variables are defined as in the general formulation. Energy FormulationThe energy equation is found by substituting energy in for N. From this, η is found to be energy per unit mass.
where Q is the heat transfer into the control volume, W is the work done by the system, g is the acceleration due to gravity, z is the vertical distance from an arbitrary datum, Note that these equations make no consideration for chemical reactions or potential energy associated with electromagnetic fields. References
Categories: Continuum mechanics | Fluid mechanics | Fluid dynamics | Chemical engineering |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Reynolds_transport_theorem". A list of authors is available in Wikipedia. |





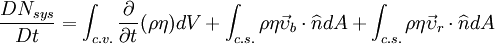 ,
,
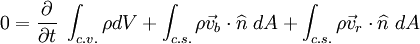
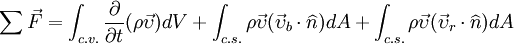 ,
,
![\dot{Q}-\sum{} \dot{W}=\int_{c.v.}^{} \frac{\partial}{\partial t} \left [ \rho \left ( \frac{\upsilon^2}{2}+gz+\tilde{u}\right ) \right ] dV + \int_{c.s.}^{} \left [\frac{\upsilon^2}{2}+gz+\tilde{u}+\frac{p}{\rho}\ \right]\rho \vec\upsilon_b\cdot\widehat{n}dA + \int_{c.s.}^{} \left [\frac{\upsilon^2}{2}+gz+\tilde{u}+\frac{p}{\rho}\ \right]\rho \vec\upsilon_r\cdot\widehat{n}dA](images/math/a/c/f/acf2a4f6d0fce66ce1ae4d1ea631f7e7.png)
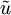 is the
is the 

