To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Control volumeIn fluid mechanics, a control volume is a mathematical abstraction employed in the process of creating mathematical models of physical processes. In an inertial frame of reference, it is a fixed volume in space through which the fluid flows. The surface enclosing the control volume is referred to as control surface. At steady state, and in the absence of work and heat transfer, a control volume can be thought of as an arbitrary volume in which the mass and the enclosed energy of the fluid remains constant. As fluid moves across the control volume, this implies that the mass entering the control volume is equal to the mass leaving the control volume. The same rule applies to the energy. Product highlight
OverviewTypically, to understand how a given physical law applies to the system under consideration, one first begins by considering how it applies to a small, control volume, or "representative volume". There is nothing special about a particular control volume, it simply represents a small part of the system to which physical laws can be easily applied. This gives rise to what is termed a volumetric, or volume-wise formulation of the mathematical model. One can then argue that since the physical laws behave in a certain way on a particular control volume, they behave the same way on all such volumes, since that particular control volume was not special in any way. In this way, the corresponding point-wise formulation of the mathematical model can be developed so it can describe the physical behaviour of an entire (and maybe more complex) system. In fluid mechanics the conservation equations (Navier-Stokes equations) are by nature integrals. They therefore apply on volumes. Finding forms of the equation that are independent of the control volumes allows simplification of the integral signs. Substantive derivativeFor understanding the substantive derivative, we might do the following simple derivation: Assuming that a control volume is filled with fluids and has the pressure p = p(x,y,z,t). At first, we take the total differential The rate of pressure change is Hence, by therefore, where References
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Control_volume". A list of authors is available in Wikipedia. |





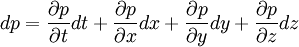
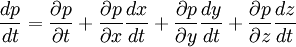
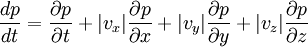
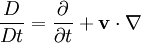
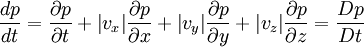
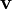 is the fluid velocity,
is the fluid velocity, is the differential operator del.
is the differential operator del.


