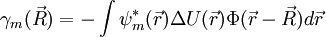To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Tight bindingIn the tight binding model, it is assumed
that the full Hamiltonian H of the system may be approximated by the
Hamiltonian of an isolated atom centred at each lattice point. The
atomic orbitals ψn, which are eigenfunctions of the single atom
Hamiltonian Hat, are assumed to be very small at distances exceeding the
lattice constant. This is what is meant by tight-binding. It is
further assumed that any corrections to the atomic potential ΔU, which are
required to obtain the full Hamiltonian H of the system, are appreciable
only when the atomic orbitals are small. A solution to the
time-independent single electron Schrödinger equation Φ is then
assumed to be a linear combination of atomic orbitals
Product highlightwhere n refers to the n-th atomic energy level and Using this approximate form for the wavefunction, and assuming only the m-th atomic energy level is important for the m-th energy band, the Bloch energies
where Em is the energy of the mth atomic level,
and are the overlap integrals.
Further reading
See also
Categories: Condensed matter physics | Quantum chemistry |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Tight_binding". A list of authors is available in Wikipedia. |


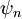
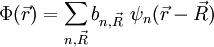 ,
,



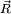 is an atomic site in the crystal lattice.
is an atomic site in the crystal lattice.
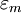 are of the form
are of the form
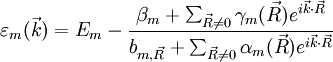 ,
,
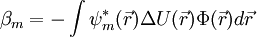 ,
,
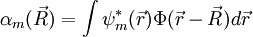 ,
,