To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Effective massIn solid state physics, a particle's effective mass is the mass it seems to carry in the semiclassical model of transport in a crystal. It can be shown that, under most conditions, electrons and holes in a crystal respond to electric and magnetic fields almost as if they were free particles in a vacuum, but with a different mass. This mass is usually stated in units of the ordinary mass of an electron me (9.11×10-31 kg). Product highlight
DefinitionWhen electron is moving inside the solid material, the force between other atoms will affect its movement and it will not be described by Newton's law. So we introduce the concept of effective mass to describe the movement of electron in Newton's law. The effective mass can be negative or different due to circumstances. Effective mass is defined by analogy with Newton's second law where a is acceleration, For a free particle, the dispersion relation is a quadratic, and so the effective mass would be constant (and equal to the real mass). In a crystal, the situation is far more complex. The dispersion relation is not even approximately quadratic, in the large scale. However, wherever a minimum occurs in the dispersion relation, the minimum can be approximated by a quadratic curve in the small region around that minimum. Hence, for electrons which have energy close to a minimum, effective mass is a useful concept. In energy regions far away from a minimum, effective mass can be negative or even approach infinity. Effective mass, being generally dependent on direction (with respect to the crystal axes), is a tensor. However, for most calculations the various directions can be averaged out. Effective mass should not be confused with reduced mass, which is a concept from Newtonian mechanics. Effective mass can only be understood with quantum mechanics. Quantum CalculationIn the free electron model, the electronic wave function can be in the form of
Now we can say: where p is the electron's momentum. Just put previous results in this last equation and we get:
Effective mass for some common semiconductors (for density of states calculations)
Sources: Experimental determinationTraditionally effective masses were measured using cyclotron resonance, a method in which microwave absorption of a semiconductor immersed in a magnetic field goes through a sharp peak when the microwave frequency equals the cyclotron frequency SignificanceAs the table shows, III-V compounds based on GaAs and InSb have far smaller effective masses than tetrahedral group IV materials like Si and Ge. In the simplest Drude picture of electronic transport, the maximum obtainable charge carrier velocity is inversely proportional to the effective mass: See also
|
|||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Effective_mass". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||||||





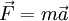 . Using quantum mechanics it can be shown that for an electron in an external electric field E:
. Using quantum mechanics it can be shown that for an electron in an external electric field E:
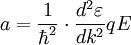
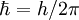 is reduced Planck's constant,
is reduced Planck's constant, 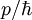 for free electrons),
for free electrons), 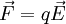 , where q is the charge. Hence under the model that only the external electric field acts, effective mass
, where q is the charge. Hence under the model that only the external electric field acts, effective mass ![m^{*} = \hbar^2 \cdot \left[ {{d^2 \varepsilon} \over {d k^2}} \right]^{-1}](images/math/4/4/f/44fe609850705ab89d76fc0714b65a4c.png)
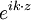 . For a wave packet the group velocity is given by:
. For a wave packet the group velocity is given by: 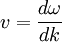 =
= 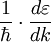
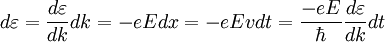
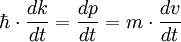
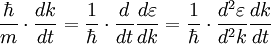
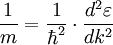
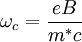 . In recent years effective masses have more commonly been determined through measurement of band structures using techniques such as angle-resolved photoemission (ARPES) or, most directly, the de Haas-van Alphen effect. Effective masses can also be estimated using the coefficient γ of the linear term in the low-temperature electronic
. In recent years effective masses have more commonly been determined through measurement of band structures using techniques such as angle-resolved photoemission (ARPES) or, most directly, the de Haas-van Alphen effect. Effective masses can also be estimated using the coefficient γ of the linear term in the low-temperature electronic 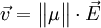 where
where 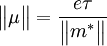 with
with 

