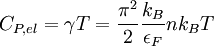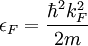Heavy Fermion

Heavy fermion materials are a specific type of metallic compounds that have a low-temperature specific heat whose linear term is up to 1000 times larger than the value expected from the free-electron theory. The heavy fermion behaviour has been found in rare earth and actinide metal compounds at very low temperatures (<10 K) in a broad variety of states including metallic, superconducting, insulating and magnetic states.

The properties of the heavy fermion compounds derive from the partly filled f-orbitals of rare earth or actinide ions which behave like localised magnetic moments. Some examples are the metal CeCu₆ and the superconductors UBe₁₃, CeAl₃ and CeCu₂Si_{_2}2. The name Heavy Fermion comes from the fact that the conduction electrons in these metallic compounds behave as if they would have an effective mass up to 1000 times the free-electron mass.

Additional recommended knowledge

Essential Laboratory Skills Guide

How to quickly check pipettes?

Recognize and detect the effects of electrostatic charges on your balance

The specific heat for normal metals

At low temperature and for normal metals, the specific heat C_P consists of the specific heat of the electrons C_P,el depending linearly on temperature T and of the the specific heat of the crystal lattice vibrations or the phonons C_P,ph depending cubically on temperature

                      CP = CP,el + CP,ph = γT + βT3

with proportionality constants β and γ.

In the temperature range mentioned above, the electronic contribution is the major part of the specific heat. For the free-electron gas -- a simple model system that neglects electron interaction -- or metals that could be described by it, the electronic specific heat is given by

with Boltzmann's factor k_B, the electron density n and the Fermi energy ε_F (the highest single particle energy of occupied electronic states). The proportionality constant γ is called the Sommerfeld parameter.

Relation between heat capacity and "thermal effective mass"

For electrons with a quadratic dispersion relation (as for the free-electron gas), the Fermi energy ε_F is inversely proportional to the particle's mass m:

where k_F stands for the Fermi wave number that depends on the electron density and is the absolute value of the wave number of the highest occupied electron state. Thus, because the Sommerfeld parameter γ is inversely proportional to ε_F, γ is proportional to the particle's mass and for high values of γ, the metal behaves as a free electron gas in which the conduction electrons have a high thermal effective mass.

Example: heat capacity for UBe₁₃ at low temperatures

Experimental results for the specific heat of the heavy fermion compound UBe₁₃ show a peak at a temperature around 0.75 K that goes down to zero with a high slope if the temperature approaches 0 K. Due to this peak, the γ-factor is much higher as for the free-electron gas in this temperature range. In contrast, above 6 K, the specific heat for this heavy fermion compound approaches the value expected from free-electron theory.

Book References

Kittel, Charles (1996) Introduction to Solid State Physics, 7th Ed., John Wiley and Sons, Inc.
Marder, M.P. (2000), Condensed Matter Physics, John Wiley & Sons, New York.
Hewson, A.C. (1993), The Kondo Problem to Heavy Fermions, Cambridge University Press.