To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Quantum Monte Carlo
Quantum Monte Carlo is a large class of computer algorithms that simulate quantum systems with the idea of solving the many-body problem. They use, in one way or another, the Monte Carlo method to handle the many dimensional integrals that arise. Quantum Monte Carlo allows a direct representation of many-body effects in the wavefunction, at the cost of statistical uncertainty that can be reduced with more simulation time. For bosons, there exist numerically exact and polynomial-scaling algorithms. For fermions, there exist very good approximations and numerically exact exponentially scaling quantum Monte Carlo algorithms, but none that are both. Product highlight
BackgroundIn principle, any physical system can be described by the many-body Schrödinger equation, as long as the constituent particles are not moving 'too' fast; that is, they are not moving near the speed of light. This includes the electrons in almost every material in the world, so if we could solve the Schrödinger equation, we could predict the behavior of any electronic system, which has important applications in fields from computers to biology. This also includes the nuclei in Bose-Einstein condensates and superfluids like liquid helium. The difficulty is that the Schrödinger equation involves a function of three times the number of particles (in 3 dimensions), and is difficult (and impossible in the case of fermions) to solve in a reasonable amount of time. Traditionally, theorists have approximated the many-body wave function as an antisymmetric function of one-body orbitals: Quantum Monte Carlo is a way around these problems because it allows us to model a many-body wave function of our choice directly. Specifically, we can use a Hartree-Fock wavefunction as our starting point, but then multiply it by any symmetric function, of which Jastrow functions are typical, designed to enforce the cusp conditions. Most methods aim at computing the ground state wave function of the system, with the exception of Path integral Monte Carlo and finite-temperature auxiliary field Monte Carlo, which calculate the density matrix.
Flavors of quantum Monte Carlo
See also
References
Lecture notes
Computer programs
Conferences, workshops, and schoolsQuantum Monte Carlo in the Apuan Alps IV - International workshop in Tuscany, Italy, 26th July-2nd August 2008 - click 'PUBLIC EVENTS' (Announcement, Poster, Sponsor). Quantum Monte Carlo and the CASINO program III - Summer school in Tuscany, Italy 3rd-10th August 2008 - click 'PUBLIC EVENTS' (Announcement, Poster). Categories: Quantum chemistry | Monte Carlo methods |
||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Quantum_Monte_Carlo". A list of authors is available in Wikipedia. |





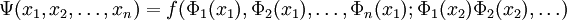 , for an example, see
, for an example, see 

