To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Density matrix renormalization groupThe density matrix renormalization group (DMRG) is a numerical variational technique devised to obtain the low energy physics of quantum manybody systems with high accuracy. It was invented in 1992 by Steven R. White and it is nowadays the most efficient method for 1D systems. Product highlight
The Idea behind DMRGThe main problem of quantum many-body physics is the fact that the Hilbert space grows exponentially with size. E.g.: for a spin-1/2 chain of length L, this dimension is 2L. The DMRG proceeds by a smart reduction of the number of effective degrees of freedom and a variational search within this reduced space. After a warmup cycle, the method splits the system into two blocks, which need not have equal sizes, and two sites in between. A set of representative states has been chosen for the block during the warmup. This set of left block + two sites + right block is known as superblock. Now a candidate for the ground state of the superblock, which is a reduced version of the full system, may be found. It may have a rather poor accuracy, but the method is iterative and it will be improved with the forthcoming steps.
The candidate ground state which has been found is projected into the subspace for each block using a density matrix, whence the name. Thus, the relevant states for each block are updated. Now one of the blocks grows at the expense of the other and the procedure is repeated. When the growing block reaches maximum size, the other starts to grow in its place. Each time we return to the original (equal sizes) situation, we say that a sweep has been completed. Normally, a few sweeps are enough to get a precision of a part in 1010.
The first application of the DMRG, by Steven White and Reinhard Noack, was a toy model: to find the spectrum of a spin 0 particle in a 1D box. It had been proposed by Kenneth G. Wilson as a test for any new renormalization group method, since they all happened to fail with this simple problem. After that, the Heisenberg model was tried, with the same accuracy. Technical details about the implementationA practical implementation of the DMRG algorithm is a lengthy work. A few of the main computational tricks are these:
ApplicationsThe DMRG has been successfully applied to get the low energy properties of spin chains: Ising model in a transverse field, Heisenberg model, etc., fermionic systems, such as the Hubbard model, problems with impurities such as the Kondo effect, boson systems, and the physics of quantum dots joined with quantum wires. It has been also extended to work on tree graphs, and has found applications in the study of dendrimers. For 2D systems with one of the dimensions much larger than the other DMRG is also accurate, and has proved useful in the study of ladders. The method has been extended to study equilibrium statistical physics in 2D, and to analyze non-equilibrium phenomena in 1D. The Matrix Product AnsatzThe success of the DMRG for 1D systems is related to the fact that it is a variational method within the space of Matrix Product States. These are states of the form
where This theory was exposed by S. Rommer and S. Ostlund in [1]. Extensions of DMRGIn 2004 the Time-evolving block decimation method was developed to implement real time evolution of Matrix Product States. The idea is based on the classical simulation of a quantum computer. Subsequently, a new method was devised to compute real time evolution within the DMRG formalism - See the paper by A. Feiguin and S.R. White [2]. In recent years, some proposals to extend the method to 2D and 3D have been put forward, extending the definition of the Matrix Product States. See this paper by F. Verstraete and I. Cirac, [3]. Further reading
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Density_matrix_renormalization_group". A list of authors is available in Wikipedia. |





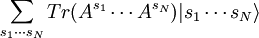
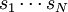 are the values of the, e.g.
are the values of the, e.g. 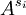 are matrices of arbitrary dimension
are matrices of arbitrary dimension 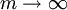 , the representation becomes exact.
, the representation becomes exact.


