Quantum wire

In condensed matter physics, a quantum wire is an electrically conducting wire, in which quantum effects are affecting transport properties. Due to the confinement of conduction electrons in the transverse direction of the wire, their transverse energy is quantized into a series of discrete values E₀ ("ground state" energy, with lower value), E₁,... (see particle in a box, quantum harmonic oscillator). One consequence of this quantization is that the classical formula for calculating the electrical resistivity of a wire:

Additional recommended knowledge

Weighing the right way

Safe Weighing Range Ensures Accurate Results

Essential Laboratory Skills Guide

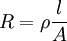is not valid for quantum wires (where ρ is the resistivity, l is the length, and A is the cross-sectional area of the wire).

Instead, an exact calculation of the transverse energies of the confined electrons has to be performed to calculate a wire's resistance. Following from the quantization of electron energy, the resistance is also found to be quantized.

The importance of the quantization is inversely proportional to the diameter of the nanowire for a given material. From material to material, it is dependent on the electronic properties, especially on the effective mass of the electrons. In simple words, it means that it will depend on how conduction electrons interact with the atoms within a given material. In practice, semiconductors show clear conductance quantization for large wire transverse dimensions (100 nm) because the electronic modes due to confinement are spatially extended. As a result their fermi wavelengths are large and thus they have low energy separations. This means that they can only be resolved at cryogenic temperature (few kelvins) where the thermal excitation energy is lower than the inter-mode energy separation.

For metals, quantization corresponding to the lowest energy states is only observed for atomic wires. Their corresponding wavelength being thus extremely small they have a very large energy separation which makes resistance quantization perfectly observable at room temperature.

Carbon nanotubes as quantum wires

It is possible to make quantum wires out of metallic carbon nanotubes, at least in limited quantities. The advantages of making wires from carbon nanotubes include their high electrical conductivity (due to a high mobility), light weight, small diameter, low chemical reactivity, and high tensile strength. The major drawback (as of 2005) is cost.

It has been claimed that it is possible to create macroscopic quantum wires. With a rope of carbon nanotubes, it is not necessary for any single fiber to travel the entire length, since quantum tunneling will allow electrons to jump from strand to strand. This makes quantum wires interesting for commercial uses.

In April 2005, NASA invested $11 million over four years with Rice University to develop quantum wire with 10 times better conductivity than copper at one-sixth the weight. It would be made with carbon nanotubes and would help reduce the weight of the next generation shuttle; but can also have wide ranging applications.

See also

• Quantum well
• Quantum dot