To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Hubbard model
The Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems. The Hubbard model, named after John Hubbard, is the simplest model of interacting particles in a lattice, with only two terms in the Hamiltonian (see example below): a kinetic term allowing for tunneling ('hopping') of particles between sites of the lattice and a potential term consisting of an on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, when the model is referred to as either the 'Bose-Hubbard model' or the 'boson Hubbard model'. The Hubbard model is a good approximation for particles in a periodic potential at sufficiently low temperatures that all the particles are in the lowest Bloch band, as long as any long-range interactions between the particles can be ignored. If interactions between particles on different sites of the lattice are included, the model is often referred to as the 'extended Hubbard model'. The model was originally proposed to describe electrons in solids and has since been the focus of particular interest as a model for high-temperature superconductivity. More recently, the Bose-Hubbard model has been used to describe the behavior of ultracold atoms trapped in optical lattices. For electrons in a solid, the Hubbard model can be considered as an improvement on the tight-binding model, which includes only the hopping term. For strong interactions, it can give qualitatively different behavior from the tight-binding model, and correctly predicts the existence of so-called Mott insulators, which are prevented from becoming conducting by the strong repulsion between the particles. Product highlight
TheoryThe Hubbard model is based on the tight-binding approximation from solid state physics. In the tight-binding approximation, electrons are viewed as occupying the standard orbitals of their constituent atoms, and then 'hopping' between atoms during conduction. Mathematically, this is represented as a 'hopping integral' or 'transfer integral' between neighboring atoms, which can be viewed as the physical principle that creates electron bands in crystalline materials. However, the more general band theories do not consider interactions between electrons. By formulating conduction in terms of the hopping integral, however, the Hubbard model is able to include the so-called 'onsite repulsion', which stems from the Coulomb repulsion between electrons. This sets up a competition between the hopping integral, which is a function of the distance and angles between neighboring atoms, and the onsite repulsion, which is not. The Hubbard model can therefore explain the transition from conductor to insulator in certain transition metal oxides as they are heated by the increase in nearest neighbor spacing, which reduces the 'hopping integral' to the point where the onsite potential is dominant. Similarly, this can explain the transition from conductor to insulator in systems such as rare-earth pyrochlores as the atomic number of the rare-earth metal increases, because the lattice parameter increases (or the angle between atoms can also change — see Crystal structure) as the rare-earth element atomic number increases, thus changing the relative importance of the hopping integral compared to the onsite repulsion. Example: 1D chain of hydrogen atomsThe hydrogen atom has only one electron, in the so-called s orbital, which can either be spin up ( Now, consider a 1D chain of hydrogen atoms. Under band theory, we would expect the 1s orbital to form a continuous band, which would be exactly half-full. The 1-D chain of hydrogen atoms is thus predicted to be a conductor under conventional band theory. But now consider the case where the spacing between the hydrogen atoms is gradually increased. At some point we expect that the chain must become an insulator. Expressed in terms of the Hubbard model, on the other hand, the Hamiltonian is now made up of two components. The first component is the hopping integral. The hopping integral is typically represented by the letter t because it represents the kinetic energy of electrons hopping between atoms. The second term in the Hubbard model is then the on-site repulsion, typically represented by the letter U because it represents the potential energy arising from the charges on the electrons. Written out in second quantization notation, the Hubbard Hamiltonian then takes the form:
If we consider the Hamiltonian without the contribution of the second term, we are simply left with the tight binding formula from regular band theory. When the second term is included, however, we end up with a more realistic model that also predicts a transition from conductor to insulator as the inter-atomic spacing is increased. In the limit where the spacing is infinite (or if we ignore the first term), the chain simply resolves into a set of isolated magnetic moments. Additionally, when there are some contributions from the first term, but the material remains an insulator, the overlap integral provides for exchange interactions between neighboring magnetic moments which may lead to a variety of interesting magnetic correlations, such as ferromagnetic, antiferromagnetic, etc. depending on the exact solutions of the model. More Complex SystemsAlthough the Hubbard model is useful in describing systems such as a 1-D chain of hydrogen atoms, it is important to note that in more complex systems there may be other effects that the Hubbard model does not consider. In general, insulators can be divided into Mott-Hubbard type insulators and charge transfer insulators. Consider the following description of a Mott-Hubbard insulator:
This can be seen as analogous to the Hubbard model for hydrogen chains, where conduction between unit cells can be described by a transfer integral. However, it is possible for the electrons to exhibit another kind of behavior:
This is known as charge transfer, and results in charge transfer insulators. Note that this is quite different from the Mott-Hubbard insulator model because there is no electron transfer between unit cells, only within a unit cell. Both of these effects may be present and competing in complex ionic systems. See alsoCategories: Condensed matter physics | Quantum chemistry | Lattice models |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Hubbard_model". A list of authors is available in Wikipedia. |





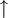 ) or spin down (
) or spin down (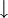 ). This orbital can be occupied by at most two electrons, one with spin up and one down (see Pauli exclusion principle).
). This orbital can be occupied by at most two electrons, one with spin up and one down (see Pauli exclusion principle).
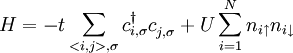 , where
, where 

