To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Bose-Hubbard modelThe Bose-Hubbard model gives an approximate description of the physics of interacting bosons on a lattice. It is closely related to the Hubbard model which originated in solid state physics as an approximate description of the motion of electrons between the atoms of a crystalline solid. However, the Hubbard model applies to fermionic particles such as electrons, rather than bosons. The Bose-Hubbard model can be used to study systems such as bosonic atoms on an optical lattice. The physics of this model is given by the Bose-Hubbard Hamiltonian: Product highlight
Here
References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Bose-Hubbard_model". A list of authors is available in Wikipedia. |





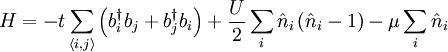 .
.
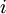 is summed over all lattice sites, and
is summed over all lattice sites, and 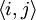 is summed over all neighboring sites.
is summed over all neighboring sites. 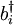 and
and 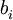 are bosonic creation and annihilation operators.
are bosonic creation and annihilation operators. 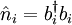 gives the number of particles on site
gives the number of particles on site 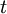 is the hopping matrix element,
is the hopping matrix element, 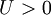 is the on site repulsion, and
is the on site repulsion, and 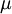 is the
is the 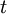 or in a
or in a 

