To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Density functional theory
Density functional theory (DFT) is a quantum mechanical theory used in physics and chemistry to investigate the ground state of many-body systems, in particular atoms, molecules and the condensed phases. DFT is among the most popular and versatile methods available in condensed matter physics, computational physics, and computational chemistry. Product highlight
PreambleThomas-Fermi modelThe predecessor to density functional theory was the Thomas-Fermi model, developed by Thomas and Fermi in 1927. They used a statistical model to approximate the distribution of electrons in an atom. The mathematical basis used was to postulate that electrons are distributed uniformly in phase space with two electrons in every h3 of volume[1]. For each element of coordinate space volume d3r we can fill out a sphere of momentum space up to the fermi momentum pf[2] equating the number of electrons in coordinate space to that in phase space gives: solving for pf and substituting in the classical kinetic energy formula then leads directly to a kinetic energy represented as a functional of the electron density: As such they were able to calculate the energy of an atom using this kinetic energy functional combined with the classical expressions for the nuclear-electron and electron-electron interactions (which can both also be represented in terms of the electron density). Although this was an important first step, the Thomas-Fermi equation's accuracy is limited because the resulting kinetic energy functional is only approximate, and also the method does not attempt to represent the exchange energy of an atom as a conclusion of the Pauli principle. An exchange energy functional was added by Dirac in 1928. However, the Thomas-Fermi-Dirac theory remained rather inaccurate for most applications. The largest source of error was in the representation of the kinetic energy, followed by the errors in the exchange energy, and due to the complete neglect of electron correlation. Teller (1962) showed that Thomas-Fermi theory cannot describe molecular bonding. This can however be overcome by improving the kinetic energy functional. The kinetic energy functional can be improved by adding the Weizsäcker (1935) correction: Hohenberg-Kohn theoremsAlthough density functional theory has its conceptual roots in the Thomas - Fermi model, DFT was not put on a firm theoretical footing until the Hohenberg-Kohn theorems (after Pierre Hohenberg and Walter Kohn) (HK). The first of these demonstrates the existence of a one-to-one mapping between the ground state electron density and the ground state wavefunction of a many-particle system. Further, the second HK theorem proves that the ground state density minimizes the total electronic energy of the system. The original HK theorems held only for the ground state in the absence of magnetic field, although they have since been generalized. The first Hohenberg-Kohn theorem is only an existence theorem, stating that the mapping exists, but does not provide any such exact mapping. It is in these mappings that approximations are made. (The theorems can be extended to the time-dependent domain (TDDFT), which can be also used to determine excited states [6].) Description of the theoryTraditional methods in electronic structure theory, in particular Hartree-Fock theory and its descendants, are based on the complicated many-electron wavefunction. The main objective of density functional theory is to replace the many-body electronic wavefunction with the electronic density as the basic quantity. Whereas the many-body wavefunction is dependent on 3N variables, three spatial variables for each of the N electrons, the density is only a function of three variables and is a simpler quantity to deal with both conceptually and practically. The most common implementation of density functional theory is through the Kohn-Sham method. Within the framework of Kohn-Sham DFT, the intractable many-body problem of interacting electrons in a static external potential is reduced to a tractable problem of non-interacting electrons moving in an effective potential. The effective potential includes the external potential and the effects of the Coulomb interactions between the electrons, e.g. the exchange and correlation interactions. Modeling the latter two interactions becomes the difficulty within KS DFT. The simplest approximation is the local-density approximation (LDA), which is based upon exact exchange energy for a uniform electron gas, which can be obtained from the Thomas-Fermi model, and from fits to the correlation energy for a uniform electron gas. DFT has been very popular for calculations in solid state physics since the 1970s. In many cases DFT with the local-density approximation gives quite satisfactory results, for solid-state calculations, in comparison to experimental data at relatively low computational costs when compared to other ways of solving the quantum mechanical many-body problem. However, it was not considered accurate enough for calculations in quantum chemistry until the 1990s, when the approximations used in the theory were greatly refined to better model the exchange and correlation interactions. DFT is now a leading method for electronic structure calculations in both fields. Despite the improvements in DFT, there are still difficulties in using density functional theory to properly describe intermolecular interactions, especially van der Waals forces (dispersion), or in calculations of the band gap in semiconductors. Its poor treatment of dispersion renders DFT unsuitable (at least when used alone) for the treatment of systems which are dominated by dispersion (e.g. interacting noble gas atoms) or where dispersion competes significantly with other effects (e.g. in biomolecules). The development of new DFT methods designed to overcome this problem, by alterations to the functional or by the inclusion of additive terms, is a current research topic. Derivation and formalismAs usual in many-body electronic structure calculations, the nuclei of the treated molecules or clusters are seen as fixed (the Born-Oppenheimer approximation), generating a static external potential V in which the electrons are moving. A stationary electronic state is then described by a wave function where H is the electronic molecular Hamiltonian, N is the number of electrons and U is the electron-electron interaction. The operators T and U are so-called universal operators as they are the same for any system, while V is system dependent or non-universal. As one can see, the actual difference between a single-particle problem and the much more complicated many-particle problem just arises from the interaction term U. There are many sophisticated methods for solving the many-body Schrödinger equation based on the expansion of the wave function in Slater determinants. While the simplest one is the Hartree-Fock method, more sophisticated approaches are usually categorized as post-Hartree-Fock methods. However, the problem with these methods is the huge computational effort, which makes it virtually impossible to apply them efficiently to larger, more complex systems. Here DFT provides an appealing alternative, being much more versatile as it provides a way to systematically map the many-body problem, with U, onto a single-body problem without U. In DFT the key variable is the particle density Hohenberg and Kohn proved in 1964 [1] that the relation expressed above can be reversed, i.e. to a given ground state density and consequently all other ground state observables From this follows, in particular, that also the ground state energy is a functional of
where the contribution of the external potential The functionals with respect to The variational problem of minimising the energy functional where Thus, one can solve the so-called Kohn-Sham equations of this auxiliary non-interacting system which yields the orbitals The effective single-particle potential where the second term denotes the so-called Hartree term describing the electron-electron Coulomb repulsion, while the last term ApproximationsThe major problem with DFT is that the exact functionals for exchange and correlation are not known except for the free electron gas. However, approximations exist which permit the calculation of certain physical quantities quite accurately. In physics the most widely used approximation is the local-density approximation (LDA), where the functional depends only on the density at the coordinate where the functional is evaluated: The local spin-density approximation (LSDA) is a straightforward generalization of the LDA to include electron spin: Highly accurate formulae for the exchange-correlation energy density
Generalized gradient approximations (GGA) are still local but also take into account the gradient of the density at the same coordinate: Using the latter (GGA) very good results for molecular geometries and ground state energies have been achieved. Many further incremental improvements have been made to DFT by developing better representations of the functionals. Generalizations to include magnetic fieldsThe DFT formalism above breaks down in the presence of a vector potential, i.e. a magnetic field. In such a case, the one-to-one mapping between electron density and external potential breaks down. Generalizations to include the effects of magnetic fields have led to two different theories: current density functional theory and magnetic field functional theory. In both these theories, the functional used for the exchange and correlation must be generalized to include more than just the electron density. In current density functional theory, developed by Vignale and Rasolt, the functionals become dependent on both the electron density and the current density. In magnetic field density functional theory, developed by Salsbury, Grayce and Harris, the functionals depend on the electron density and the magnetic field, and the functional form can depend on the form of the magnetic field. In both of these theories it has been difficult to develop functionals beyond their equivalent to LDA, which are also readily implementable computationally. ApplicationsIn practice, Kohn-Sham theory can be applied in several distinct ways depending on what is being investigated. In solid state calculations, the local density approximations are still commonly used along with plane wave basis sets, as an electron gas approach is more appropriate for an infinite solid. In molecular calculations, however, more sophisticated functionals are needed, and a huge variety of exchange-correlation functionals have been developed for chemical applications. Some of these are inconsistent with the uniform electron gas approximation, however, they must reduce to LDA in the electron gas limit. Among physicists, probably the most widely used functional is the revised Perdew-Burke-Ernzerhof exchange model (a direct generalized-gradient parametrization of the free electron gas with no free parameters); however, this is not sufficiently calorimetrically accurate for gas-phase molecular calculations. In the chemistry community, one popular functional is known as BLYP (from the name Becke for the exchange part and Lee, Yang and Parr for the correlation part). Even more widely used is B3LYP [3-5] which is a hybrid functional in which the exchange energy, in this case from Becke's exchange functional, is combined with the exact energy from Hartree-Fock theory. Along with the component exchange and correlation funсtionals, three parameters define the hybrid functional, specifying how much of the exact exchange is mixed in. The adjustable parameters in hybrid functionals are generally fitted to a 'training set' of molecules. Unfortunately, although the results obtained with these functionals are usually sufficiently accurate for most applications, there is no systematic way of improving them (in contrast to some of the traditional wavefunction-based methods like configuration interaction or coupled cluster theory). Hence in the current DFT approach it is not possible to estimate the error of the calculations without comparing them to other methods or experiments. Software supporting DFT
Books on DFT
Key papers
References
Categories: Density functional theory | Computational chemistry | Quantum chemistry |
|||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Density_functional_theory". A list of authors is available in Wikipedia. |





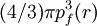
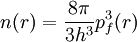
![T_{TF}[n]=C_F\int n^{5/3}(r) d^3r.](images/math/e/5/4/e54c910ae6f9a749a0c29c97a1c61578.png)
![T_W[n]=\frac{1}{8}\frac{\hbar^2}{m}\int\frac{|\nabla n(r)|^2}{n(r)}dr](images/math/6/3/5/635a79018ee06cd0c59802c7b933ad76.png)
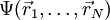 fulfilling the many-electron Schrödinger equation
fulfilling the many-electron Schrödinger equation
![H \Psi = \left[{T}+{V}+{U}\right]\Psi = \left[\sum_i^N -\frac{\hbar^2}{2m}\nabla_i^2 - \sum_i^N V(\vec r_i) + \sum_{i<j}U(\vec r_i, \vec r_j)\right] \Psi = E \Psi](images/math/0/b/2/0b2036ddca92a3c5b9333386f8234d6e.png)
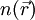 which is given by
which is given by
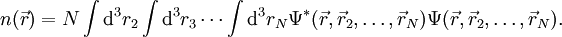
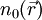 it is in principle possible to calculate the corresponding ground state wavefunction
it is in principle possible to calculate the corresponding ground state wavefunction 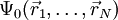 . In other words,
. In other words, 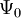 is a unique functional of
is a unique functional of 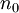 , i.e.
, i.e.
![\,\!\Psi_0 = \Psi_0[n_0]](images/math/9/1/4/91494d588a559664466a8868e013cd83.png)
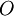 are also functionals of
are also functionals of ![\left\langle O \right\rangle[n_0] = \left\langle \Psi_0[n_0] \left| O \right| \Psi_0[n_0] \right\rangle.](images/math/d/d/f/ddf161238882c4132ca78d8b97992618.png)
![E_0 = E[n_0] = \left\langle \Psi_0[n_0] \left| T+V+U \right| \Psi_0[n_0] \right\rangle](images/math/f/1/0/f104ef95198fdaf6bc10545548ae1d22.png) ,
,
![\left\langle \Psi_0[n_0] \left|V\right| \Psi_0[n_0] \right\rangle](images/math/b/4/3/b43603abb4d16c6fea7731e8355c3148.png) can be written explicitly in terms of the density
can be written explicitly in terms of the density
![V[n] = \int V(\vec r) n(\vec r){\rm d}^3r.](images/math/5/7/9/5795bfad63753d0007ec32019fc2ef18.png)
![\,\!T[n]](images/math/2/2/2/2220bca035dc1ca4b3c43a0465cf7de4.png) and
and ![\,\!U[n]](images/math/8/c/3/8c380361593608570ffd1e2013557443.png) are called universal functionals while
are called universal functionals while ![\,\!V[n]](images/math/b/4/0/b40fbd957f5970efeed776fa2de69c73.png) is obviously non-universal, as it depends on the system under study. Having specified a system, i.e.
is obviously non-universal, as it depends on the system under study. Having specified a system, i.e. 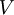 is known, one then has to minimise the functional
is known, one then has to minimise the functional
![E[n] = T[n]+ U[n] + \int V(\vec r) n(\vec r){\rm d}^3r](images/math/a/7/7/a77376c23cf64fcf19999bb0f021d90f.png)
![\,\!E[n]](images/math/5/1/9/51999f8192d36af3a519560759a0ef40.png) can be solved by applying the Lagrangian method of undetermined multipliers, which was done by Kohn and Sham in 1965 [2]. Hereby, one uses the fact that the functional in the equation above
can be written as a fictitious density functional of a non-interacting system
can be solved by applying the Lagrangian method of undetermined multipliers, which was done by Kohn and Sham in 1965 [2]. Hereby, one uses the fact that the functional in the equation above
can be written as a fictitious density functional of a non-interacting system
![E_s[n] = \left\langle \Psi_s[n] \left| T_s+V_s \right| \Psi_s[n] \right\rangle,](images/math/a/a/2/aa291aa63729fd07d10cda5ef70d8234.png)
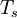 denotes the non-interacting kinetic energy and
denotes the non-interacting kinetic energy and 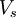 is an external effective potential in which the particles are moving. Obviously,
is an external effective potential in which the particles are moving. Obviously,  if
if 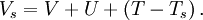
![\left[-\frac{\hbar^2}{2m}\nabla^2+V_s(\vec r)\right] \phi_i(\vec r) = \epsilon_i \phi_i(\vec r),](images/math/c/9/a/c9a797a1b4d0b830dd45383af75b9142.png)
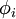 that reproduce the density
that reproduce the density 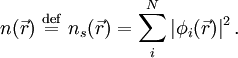
![V_s = V + \int \frac{e^2n_s(\vec r\,')}{|\vec r-\vec r\,'|} {\rm d}^3r' + V_{\rm XC}[n_s(\vec r)],](images/math/4/d/1/4d1c9d57776ca10dd74eb11970b18626.png)
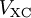 is called the exchange correlation potential. Here,
is called the exchange correlation potential. Here, ![E_{XC}[n]=\int\epsilon_{XC}(n)n (r) {\rm d}^3r.](images/math/4/6/2/462f3ba936e9b0855a5ab0e2392ad404.png)
![E_{XC}[n_\uparrow,n_\downarrow]=\int\epsilon_{XC}(n_\uparrow,n_\downarrow)n (r){\rm d}^3r.](images/math/c/4/0/c4082bd09b6e7b40d6eaed869e602a75.png)
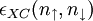 have been constructed
from
have been constructed
from ![E_{XC}[n_\uparrow,n_\downarrow]=\int\epsilon_{XC}(n_\uparrow,n_\downarrow,\vec{\nabla}n_\uparrow,\vec{\nabla}n_\downarrow) n (r) {\rm d}^3r.](images/math/0/d/8/0d88614d9d8d94f46bc37780c3e0a4fd.png)


