To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Local-density approximationThe local-density approximation (LDA) is an approximation of the exchange-correlation (XC) energy functional in density functional theory (DFT) by taking the XC energy of an electron in a non-interacting homogeneous electron gas of a density equivalent to the density at the electron in the system being calculated. This approximation was applied to DFT by Kohn and Sham in an early paper.[1] Product highlightThe Hohenberg-Kohn theorem states that the energy of the ground state of a system of electrons is a functional of the electronic density, in particular the exchange and correlation energy is also a functional of the density (this energy can be seen as the quantum part of the electron-electron interaction). This XC functional is not known exactly and must be approximated.[2] LDA is the simplest approximation for this functional, it is local in the sense that the electron exchange and correlation energy at any point in space is a function of the electron density at that point only.[3] The LDA functional assumes that the per-electron exchange-correlation energy at every point in space is equal to the per-electron exchange-correlation energy of a homogeneous electron gas.[1] The XC correlation functional is the sum of a correlation functional and an exchange functional[1] ExchangeLDA uses the exchange for the uniform electron gas of a density equal to the density at the point where the exchange is to be evaluated, in SI units where CorrelationThere are several forms of correlation:
Wigner correlation is gotten by using equally spaced electrons and applying perturbation theory.[5] VWN, PZ and PW92 are fit to a quantum Monte Carlo calculation[12] of the electron gas at varying densities.[11] LYP is based on data fit to the helium atom.[10] References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Local-density_approximation". A list of authors is available in Wikipedia. |





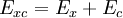
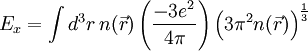
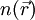 is the electron density per unit volume at the point
is the electron density per unit volume at the point 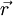 and
and 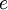 is the charge of an electron.
is the charge of an electron.

