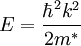To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Free electron modelIn solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics. Given its simplicity, it is surprisingly successful in explaining many experimental phenomena, especially
Product highlight
Ideas and assumptionsAs in the Drude model, valence electrons are assumed to be completely detached from their ions ("electron gas"). As in an ideal gas, electron-electron interactions are completely neglected (they are weak because of the shielding effect). The crystal lattice is not explicitly taken into account. A quantum-mechanical justification is given by Bloch's Theorem: an unbound electron moves in a constant periodic potential as a free electron in vacuum, except for the electron mass m becoming an effective mass m* which may deviate considerably from m (one can even use negative effective mass to describe conduction by electron holes). Effective masses can be derived from band structure computations. While the static lattice does not hinder the motion of the electrons, they can well be scattered by impurities and by phonons; these two interactions determine electrical and thermal conductivity (superconductivity requires more refined theory than the free electron model). According to the Pauli exclusion principle, each phase space element (Δk)3(Δx)3 can be occupied only by two electrons (one per spin quantum number). This restriction of available electron states is taken into account by Fermi-Dirac statistics (see also Fermi gas). Main predictions of the free electron model are derived by the Sommerfeld expansion of the Fermi-Dirac occupancy for energies around the Fermi level. TechnicalitiesEffective massA band structure computation actually yields a dispersion relation E(k) between electron wave vector k and energy E. An effective mass is obtained by approximating the true dispersion relation in the limit of small k by the free-electron form (with the free-electron mass m replaced by m*). A lattice electron with a fictitious mass can be seen as a quasiparticle (though there is a one-to-one correspondence to the real particle which is not the case for other quasiparticles such as phonons). Relation with other electron modelsThe assumption of electrons that move freely through a periodic potential should be contrasted with the tight-binding model, which uses the opposite simplification of treating the electrons as tightly bound to the atomic cores. (Coulomb interactions between electrons are still neglected.) The predictions of these two complementary models are reassuringly similar. Taking into account the specifities of the potential in a real, three-dimensional crystal lattice leads to more complicated dispersion relations and to band theory. See alsoExternal articles and references
Categories: Condensed matter physics | Electron |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Free_electron_model". A list of authors is available in Wikipedia. |