To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Time-dependent density functional theoryTime-dependent density functional theory (TDDFT) is a quantum mechanical method used in physics and chemistry to investigate the proprieties of many-body systems beyond the ground state structure. It's an extension of density functional theory (DFT) to the time-dependent domain as a method to describe such systems when a time dependent perturbation is applied and, as DFT, it's becoming one of the the most popular and versatile methods available in condensed matter physics, computational physics, and computational chemistry. The main ideas of such approach are the same we can find in DFT being the density of the system, at least in the first formulation of the method, the key quantity. So, respect to the direct quantum mechanical approach, one has to play with a single variable quantity and not with the multi-variable wave-function. Still as for the ground state approach one can construct a Kohn-Sham (KS) time dependent systems of non interacting particles which gives the same density of the physical interacting system and in which all the effects of the interaction are shifted in a local effective potential. The main difference here with respect to DFT is that the exact effective potential in a generic instant will depend on the density of the systems at all the previous instants. The main success of TDDFT till now has been its application in the calculation of electron excited states, mainly for isolated systems, where the method is used in the linear regime domain. The excited states energies can be computed as the poles of the response function of the system which can be computed using a Dyson equation. The key ingredients become the KS not interacting response function and the Hartree plus exchange-correlation kernel which is the functional derivative of the effective potential with respect to the density. As for DFT one has to do approximations. The most popular is the adiabatic approximation which is the respective of the Local Density Approximation (LDA) in the time domain, so that the effective potential in a generic instant depends only the density of the systems at that instant; the excitation's energies are usually computed within Adiabatic + Local Density approximation (ALDA). The results are quite good but still the approach suffer of some problems, some of which are due to the errors in the DFT/LDA ground state calculation, as the underestimation ionization energy, some others which are due to the adiabatic approximation, such as the lack of multi-electron excitations within this approximation. The equations of TDDFT rely on the Runge-Gross theorem (1984) which is the time-dependent analog of the Hohenberg-Kohn theorem (1964) for DFT. The complete theorem is valid only for isolated systems, while for periodic infinite systems one as to use some more general approach as for example Time Dependet Current Density Functional Theory (TDCDFT) developed by Vignale, in which the fundamental quantity is the current density. Product highlight
Formalism of TDDFTIntroductionConsider a many body system described by the Hamiltonian:
where T is the kinetic energy, Vext is an external potential
and W is a two body operator which describe the interaction among the particles
of your system. We will call this the physical system of our model.
To fix the ideas you can imagine that we are describing the electrons of
a molecule keeping the ions in a fixed position, so that T is the kinetic energy
of the electrons, Vext is the potential due to the ions and
for which the ground-state density of the interacting system is equal to the ground state
density of the KS system: Now Runge-Gross theorem extend the validity of this relation even to time dependent domain, so that if we apply a time dependent external perturbation to our system we will have
where now the identity will holds for Linear response TDDFTLinear response TDDFT can be used if we consider the external perturbation to be small in the sense that it does not completely destruct the ground state structure of our system. In this case we can look at the linear response of the system. This is a great advantage as, to first order, the variation of the system will depend only on the ground state wave-function so that we can simply use all the ingredients of DFT. So consider a small time dependent external perturbation δVext(t). We will have
and looking at the linear response of the density where δVeff[ρ](t) = δVext(t) + δVH[ρ](t) + δVxc[ρ](t) Here and in the following we will intend that primed variables are integrated. Being in linear response domain we can now expand the variation of the Hartree (H) and the exchange-correlation (xc) potential to linear order respect to the density variation and Finally inserting this relation in the response equation for the KS system and comparing the resultant equation with the response equation for the physical system we get the Dyson equation of TDDFT: From this last equation it's possible to derive the excitations energies of our system, being them the poles of the response function. Key papers
Books on TDDFT
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Time-dependent_density_functional_theory". A list of authors is available in Wikipedia. |
- Trichoderma
- Alu_sequence
- Chemical_synapse
- Potentially harmful chemicals found in plastic toys - New research suggests that more than 100 chemicals found in plastic toy materials may pose possible health risks to children
- e-Book: Uno sguardo interno agli aggiornamenti della UL 9540A:2025 - Scoprite i principali aggiornamenti della UL 9540A:2025, tra cui i metodi di prova migliorati e altro ancora





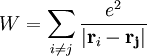 is the coulomb interaction
among the electrons. According to
is the coulomb interaction
among the electrons. According to 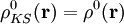 . Here the
superscript zero stands for ground-state and
. Here the
superscript zero stands for ground-state and 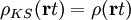 assuming that at time
assuming that at time 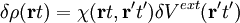
](images/math/c/6/9/c69eec3b905624fd8453bae3972d48a6.png)
=\frac{\delta V_H[\rho]}{\delta\rho}\delta\rho= \frac{1}{|\mathbf{r}-\mathbf{r'}|}\delta\rho(\mathbf{r'})](images/math/2/7/c/27c215fd19be84550d69b257059bfe6d.png)
=\frac{\delta V_{xc}[\rho]}{\delta\rho}\delta\rho= f_{xc}(\mathbf{r}t,\mathbf{r'}t')\delta\rho(\mathbf{r'})](images/math/e/0/d/e0df9bf6005b397b36115657a0feb8ca.png)