To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Band gapIn solid state physics and related applied fields, the band gap, also called an energy gap or stop band, is a region where a particle or quasiparticle is forbidden from propagating. For insulators and semiconductors, the band gap generally refers to the energy difference between the top of the valence band and the bottom of the conduction band. Product highlight
In semiconductor physics
In semiconductors and insulators, electrons are confined to a number of bands of energy, and forbidden from other regions. The term "band gap" refers to the energy difference between the top of the valence band and the bottom of the conduction band; electrons are able to jump from one band to another. The conductivity of intrinsic semiconductors is strongly dependent on the band gap. The only available carriers for conduction are the electrons which have enough thermal energy to be excited across the band gap. Band gap engineering is the process of controlling or altering the band gap of a material by controlling the composition of certain semiconductor alloys, such as GaAlAs, InGaAs, and InAlAs. It is also possible to construct layered materials with alternating compositions by techniques like molecular beam epitaxy. These methods are exploited in the design of heterojunction bipolar transistors (HBTs), laser diodes and solar cells. The distinction between semiconductors and insulators is a matter of convention. One approach is to consider semiconductors a type of insulator with a low band gap. Insulators with a higher band gap, usually greater than 3 eV, are not considered semiconductors and generally do not exhibit semiconductive behaviour under practical conditions. Electron mobility also plays a role in determining a material's informal classification. Band gaps depend on temperature because of thermal expansion. Band gaps also depend on pressure. Band gaps can be either direct or indirect bandgaps, depending on the band structure. Mathematical interpretationClassically, the ratio of probabilities that two states with an energy difference ΔE will be occupied by an electron is given by the Boltzmann factor: where:
At the Fermi level (or chemical potential), the probability of a state being occupied is ½. If the Fermi level is in the middle of a band gap of 1 eV, this ratio is e -20 or about 0.5•10-9 at the room-temperature thermal energy of 25 meV. List of band gaps
In photonics and phononicsIn photonics band gaps or stop bands are ranges of photon frequencies where, if tunneling effects are neglected, no photons can be transmitted through a material. A material exhibiting this behaviour is known as a photonic crystal. Similar physics applies to phonons in a phononic crystal. References
See alsoChemicals
List of electronics topics
Categories: Condensed matter physics | Semiconductors |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Band_gap". A list of authors is available in Wikipedia. |





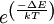
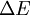 is the energy difference
is the energy difference
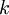 is
is 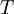 is
is 

