To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Kohn-Sham equationsThe Kohn-Sham equations are a set of eigenvalue equations within density functional theory (DFT). DFT attempts to reduce a many-body problem for the N particle wavefunction
Product highlightwhere T is the kinetic energy of the system, Vext is an external potential acting on the system, is the Hartree energy and Exc is the exchange-correlation energy. The straightforward application of this formula has two obstacles: first, the exchange-correlation energy is not known exactly (see DFT Approximations for the workaround), and second, the kinetic term must be formulated in terms of the charge density. As was first proposed by Kohn and Sham, the charge density can be written as the sum of the squares of a set of orthonormal wave functions which are solutions to the Schrödinger equation for N noninteracting electrons moving in an effective potential where the effective potential is defined to be These three equations form the Kohn-Sham orbital equations in their canonical form. This system is then solved iteratively, until self-consistency is reached. Note that the eigenvalues εi have no physical meaning, only the total sum, which corresponds to the energy of the entire system E through the equation
References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Kohn-Sham_equations". A list of authors is available in Wikipedia. |


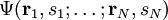 (which depends on 4N variables) to one in terms of the charge density
(which depends on 4N variables) to one in terms of the charge density 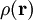 (which depends on 3 variables), using the
(which depends on 3 variables), using the ![E[\rho] = T[\rho] + \int V_{ext}(\mathbf{r}) \rho(\mathbf{r}) d\mathbf{r} + V_{H}[\rho] + E_{xc}[\rho] \,\;](images/math/e/e/c/eec82ed32f3cc7949e5d1d8f7c899a40.png) ,
,



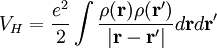
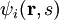 :
:
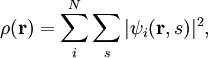
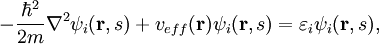
![v_{eff}(\mathbf{r}) = V_{ext}(\mathbf{r}) + e^2\int {\rho(\mathbf{r}')\over|\mathbf{r}-\mathbf{r}'|}d\mathbf{r}' + {\delta E_{xc}[\rho]\over\delta\rho}.](images/math/0/0/8/00827e69f15fac533f19e5bc8d25a0b2.png)
![E = \sum_{i}^N \varepsilon_i - V_{H}[\rho] + E_{xc}[\rho] - \int {\delta E_{xc}[\rho]\over\delta \rho(\mathbf{r})} \rho(\mathbf{r}) d\mathbf{r}](images/math/7/4/9/749a921e4171aa4318fc0cdd5e8a9da2.png) .
.


