Hybrid functional

A hybrid functional is an exchange-correlation functional used in density functional theory (DFT) that incorporates a portion of exact exchange from Hartree-Fock theory with exchange and correlation from other sources (ab initio, such as LDA, or empirical).

Additional recommended knowledge

What is the Correct Way to Check Repeatability in Balances?

How to quickly check pipettes?

Daily Visual Balance Check

Origin

The hybrid approach to density functionals was first introduced by Axel Becke in 1993^[1]. Hybridization with Hartree-Fock (exact) exchange provides a simple scheme for improving many molecular properties, such as atomization energies, bond lengths and vibration frequencies, which tend to be poorly described with simple ab initio functionals.^[2]

Method

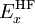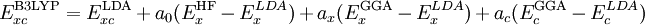
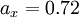The exchange-correlation functional for a hybrid is usually a linear combination of the Hartree-Fock exchange () and some other one or combination of exchange and correlation functionals. The parameter(s) relating the amount of each functional can be arbitrarily assigned and is usually fitted to reproduce well some set of observables (bond lengths, band gaps, etc.). For example, the popular B3LYP (Becke, three-parameter, Lee-Yang-Parr)^[3][4] exchange-correlation functional is:

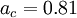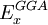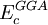where , , and are the three empirical parameters; and are the generalized gradient approximation formulated with the Becke 88 exchange functional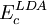^[5] and the correlation functional of Lee, Yang and Parr^[6], and the VWN correlation functional (see Local-density approximation#Correlation).

List of hybrid functionals (in Gaussian 03)

• B3LYP
• B3P86
• B1B95
• B1LYP
• MPW1PW91
• B97
• B98
• B971
• B972
• PBE1PBE
• O3LYP
• BHandH
• BHandHLYP
• BMK

See: G03 Manual: DFT.

References

1. ^ A.D. Becke (1993). "A new mixing of Hartree-Fock and local density-functional theories". J. Chem. Phys. 98: 1372-1377.
2. ^ John P. Perdew, Matthias Ernzerhof and Kieron Burke (1996). "Rationale for mixing exact exchange with density functional approximations". J. Chem. Phys. 105: 9982-9985.
3. ^ K. Kim and K. D. Jordan (1994). "Comparison of Density Functional and MP2 Calculations on the Water Monomer and Dimer". J. Phys. Chem. 98 (40): 10089 - 10094.
4. ^ P.J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch (1994). "Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields". J. Phys. Chem. 98: 11623 - 11627. doi:10.1021/j100096a001.
5. ^ A. D. Becke (1988). "Density-functional exchange-energy approximation with correct asymptotic behavior". Phys. Rev. A 38: 3098 - 3100. doi:10.1103/PhysRevA.38.3098.
6. ^ Chengteh Lee, Weitao Yang and Robert G. Parr (1988). "Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density". Phys. Rev. B 37: 785.