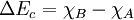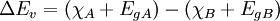Anderson's rule

Anderson's rule is used for the construction of energy band diagrams of the heterojunction between two semiconductor materials. It is also referred to as the electron affinity rule. Anderson's rule was first described by R. L. Anderson in 1960 (Anderson, 1960).

Additional recommended knowledge

Better weighing performance in 6 easy steps

Daily Sensitivity Test

Safe Weighing Range Ensures Accurate Results

Anderson's rule states that when constructing an energy band diagram, the vacuum levels of the two semiconductors on either side of the heterojunction should be aligned (at the same energy) (Borisenko and Ossicini, 2004).

Using Anderson's rule to construct energy band diagrams

Once the vacuum levels are aligned it is possible to use the electron affinity and band gap values for each semiconductor to calculate the conduction band and valence band offsets (Davies, 1997). The electron affinity (usually given the symbol χ in solid state physics) gives the energy difference between the lower edge of the conduction band and the vacuum level of the semiconductor. The band gap (usually given the symbol E_g) gives the energy difference between the lower edge of the conduction band and the upper edge of the valence band. Each semiconductor has different electron affinity and band gap values. For semiconductor alloys it may be necessary to use Vegard's law to calculate these values.

Once the relative positions of the conduction and valence bands for both semiconductors are known, Anderson's rule allows the calculation of the band offsets of both the valence band (ΔE_v) and the conduction band (ΔE_c).

Consider a heterojunction between semiconductor A and semiconductor B. Suppose the conduction band of semiconductor A lies at a higher energy than that of semiconductor B. The conduction band offset would then be given by:

Then suppose that the band gap of semiconductor A is large enough that the valence band of semiconductor B lies at a higher energy than that of semiconductor A, then the valence band offset is given by:

Poisson’s equation can then be used to calculate the band bending between the two semiconductors.

References

Anderson, R. L., (1960). Germanium-gallium arsenide heterojunction, IBM J. Res. Dev. 4(3), pp. 283-287

Borisenko, V. E. and Ossicini, S. (2004). What is What in the Nanoworld: A Handbook on Nanoscience and Nanotechnology. Germany: Wiley-VCH.

Davies, J. H., (1997). The Physics of Low-Dimensional Semiconductors. UK: Cambridge University Press.