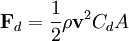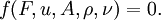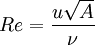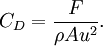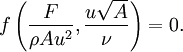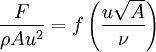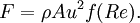To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Drag equationThe drag equation is a practical formula used to calculate the force of drag experienced by an object due to a fluid that it is moving through. The equation is attributed to Lord Rayleigh, who originally used where
The reference area A is the area of the projection of the object on a plane perpendicular to the direction of motion (ie cross-sectional area). Sometimes different reference areas are given for the same object in which case a drag coefficient corresponding to each of these different areas must be given. The reference for a wing would be the plane area rather than the frontal area. Product highlight
DiscussionThe equation is based on an idealized situation where all of the fluid impinges on the reference area and comes to a complete stop, building up stagnation pressure over the whole area. No real object exactly corresponds to this behavior. Cd is the ratio of drag for any real object to that of the ideal object. In practice a rough unstreamlined body (a bluff body) will have a Cd around 1, more or less. Smoother objects can have much lower values of Cd. The equation is precise--it simply provides the definition of Cd (drag coefficient), which varies with the Reynolds number and is found by experiment. Of particular importance is the v² dependence on velocity, meaning that fluid drag increases with the square of velocity. When velocity is doubled, for example, not only does the fluid strike with twice the velocity, but twice the mass of fluid strikes per second. Therefore the change of momentum per second is multiplied by four. Force is equivalent to the change of momentum divided by time. This is in contrast with solid-on-solid friction, which generally has very little velocity dependence. DerivationThe drag equation may be derived to within a multiplicative constant by the method of dimensional analysis. If a moving fluid meets an object, it exerts a force on the object, according to a complicated (and not completely understood) law. We might suppose that the variables involved under some conditions to be the speed, density and viscosity of the fluid, the size of the body (expressed in terms of its frontal area A), and the drag force. Using the algorithm of the Buckingham π theorem, one can reduce these five variables to two dimensionless parameters: the drag coefficient and the Reynolds number. Alternatively, one can derive the dimensionless parameters via direct manipulation of the underlying differential equations. That this is so becomes obvious when the drag force F is expressed as part of a function of the other variables in the problem: This rather odd form of expression is used because it does not assume a one-to-one relationship. Here, f is some (as-yet-unknown) function that takes five arguments. We note that the right-hand side is zero in any system of units; so it should be possible to express the relationship described by f in terms of only dimensionless groups. There are many ways of combining the five arguments of f to form dimensionless groups, but the π-theorem states that there will be two such groups. The most appropriate are the Reynolds number, given by and the drag coefficient, given by Thus the function of five variables may be replaced by another function of only two variables: where f is some function of two arguments. The original law is then reduced to a law involving only these two numbers. Because the only unknown in the above equation is F, it is possible to express it as or Thus the force is simply ρAu2 times some (as-yet-unknown) function of the Reynolds number—a considerably simpler system than the original five-argument function given above. Dimensional analysis thus makes a very complex problem (trying to determine the behavior of a function of five variables) a much simpler one: the determination of the drag as a function of only one variable, the Reynolds number. The analysis also gives other information for free, so to speak. We know that, other things being equal, the drag force will be proportional to the density of the fluid. This kind of information often proves to be extremely valuable, especially in the early stages of a research project. To empirically determine the Reynolds number dependence, instead of experimenting on huge bodies with fast-flowing fluids (such as real-size airplanes in wind-tunnels), one may just as well experiment on small models with slow-flowing, more viscous fluids, because these two systems are similar. References
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Drag_equation". A list of authors is available in Wikipedia. |


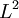 in place of
in place of 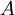 (L being some linear dimension). The force on a moving object due to a fluid is:
(L being some linear dimension). The force on a moving object due to a fluid is: