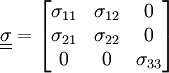Plane strain

In real engineering components, stress (and strain) are 3-D tensors but in prismatic structures such as a long metal billet, the length of the structure is much greater than the other two dimensions. The strains associated with length, i.e the normal strain ε₃₃ and the shear strains ε₁₃ and ε₂₃ (if the length is the 3-direction) are constrained by nearby material and are small compared to the cross-sectional strains. The strain tensor can then be approximated by:

Additional recommended knowledge

Better weighing performance in 6 easy steps

Daily Sensitivity Test

Guide to balance cleaning: 8 simple steps

in which the double underline indicates a second order tensor. This strain state is called plane strain. The corresponding stress tensor is:

in which the non-zero σ₃₃ is needed to maintain the constraint ε₃₃ = 0. This stress term can be temporarily removed from the analysis to leave only the in-plane terms, effectively reducing the 3-D problem to a much simpler 2-D problem.

See also plane stress.