To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Plane stressIn real engineering components, stress (and strain) are 3-D tensors, however when one of the dimensions of the material is much smaller than the other two, it can be neglected and the resulting state of stress becomes bidimensional.[1] This state is known as plane stress because the normal, σ33, and shear, σ13 and σ23, stresses with respect to the thin surface are zero. Examples of such materials include thin-walled structures such as plates subject to in-plane loading or thin cylinders subject to pressure loading. The stresses are negligible with respect to the smaller dimension because the stresses are not able to develop within the material and are small compared to the in-plane stresses.[1] Product highlightUsing the generalized form of Hooke's law: εxx = (σxx / E) where E is the Young's modulus of elasticity, and combining this with the principle of superposition, we obtain: εxx = ((1 / E)[σxx − ν(σyy + σzz)]) where ν is poisson's ratio, which can be used to calculate various components of the stress or strain state. Additionally, the stress tensor can then be approximated by:
in which the double underline indicates a second order tensor. This stress state is called plane stress. The corresponding strain tensor is: in which the non-zero ε33 term arises from the Poisson's ratio effect. This strain term can be temporarily removed from the analysis to leave only the in-plane terms, effectively reducing the 3-D problem to a much simpler 2-D problem. Moreover, this can graphically be represented using Mohr's circle, which is a graphical solution of a biaxial state of stress. Mohr's circle is most notably used for making stress transformations in a 2-D and even 3-D state.[1] See alsoReferencesMeyers and Chawla (1999): "Mechanical Behavior of Materials," 66-75. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Plane_stress". A list of authors is available in Wikipedia. |





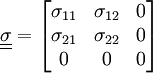 .
.



