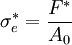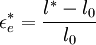To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Compressive strengthCompressive strength is the capacity of a material to withstand axially directed pushing forces. When the limit of compressive strength is reached, materials are crushed. Concrete can be made to have high compressive strength, e.g. many concrete structures have compressive strengths in excess of 50 MPa, whereas a material such as soft sandstone may have a compressive strength as low as 5 or 10 MPa. Compare tensile strength. Product highlight
Introduction
When a specimen of material is loaded in such a way that it extends it is said to be in tension. On the other hand if the material compresses and shortens it is said to be in compression. On an atomic level, the molecules or atoms are forced apart when in tension whereas in compression they are forced together. Since atoms in solids always try to find an equilibrium position and distance between other atoms forces arise throughout the entire material which oppose both tension or compression. The phenomena prevailing on an atomic level are therefore similar. On a macroscopic scale, these aspects are also reflected in the fact that the properties of materials in tension and compression are quite similar, at least for most materials. Of course, the major difference between the two types of loading is the strain which would have opposite signs for tension (positive) and compression (negative). Compressive StrengthBy definition, the compressive strength of a material is that value of uniaxial compressive stress reached when the material fails completely. The compressive strength is usually obtained experimentally by means of a compressive test. The apparatus used for this experiment is the same as that used in a tensile test. However, rather than applying a uniaxial tensile load, a uniaxial compressive load is applied. As can be imagined, the specimen (Usually cylindrical) is shortened as well as spread laterally. A Stress–strain curve is plotted by the instrument and would look similar to the following: The compressive strength of the material would correspond to the stress at the red point shown on the curve. Even in a compression test, there is a linear region where the material follows Hooke's Law. Hence for this region σ = Eε where this time E refers to the Young's Modulus for compression. This linear region terminates at what is known as the yield point. Above this point the material behaves plastically and will not return to its original length once the load is removed. There is a difference between the engineering stress and the true stress. By its basic definition the uniaxial stress is given by:
where, F = Load applied [N], A = Area [m2] As we said, the area of the specimen varies on compression. In reality therefore the area is some function of the applied load i.e. A = f(F). Indeed, we can however say that the stress is defined as the force divided by the area at the start of the experiment. This is known as the engineering stress and is defined by,
A0=Original specimen area [m2]
where l = current specimen length [m] and l0 = original specimen length [m] The compressive stress would therefore correspond to the point on the engineering stress strain curve
where F* = load applied just before crushing and l* = specimen length just before crushing. Deviation of engineering stress from true stressIn engineering design practice we mostly rely on the engineering stress. In reality, the true stress is different from the engineering stress. Hence calculating the compressive strength of a material from the given equations will not yield an accurate result. This is of course due to the fact that the cross sectional area A0 changes and is some function of load A = φ(F). The difference in values may therefore be summarized as follows:
As a final note, it should be mentioned that the frictional force mentioned in the second point is not constant for the entire cross section of the specimen. It varies from a minimum at the centre to a maximum at the edges. Due to this a phenomenon known as barrelling occurs where the specimen attains a barrel shape (hence its name). See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Compressive_strength". A list of authors is available in Wikipedia. |





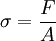
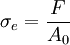
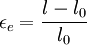
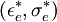 defined by
defined by