To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Inexact differentialIn thermodynamics, an inexact differential or imperfect differential is any quantity, particularly heat Q and work W, that are not state functions, in that their values depend on how the process is carried out.[1] The symbol , or δ (in the modern sense), which originated from the work of German mathematician Carl Gottfried Neumann in his 1875 Vorlesungen uber die mechanische Theorie der Warme, indicates that Q and W are path dependent.[1] In terms of infinitesimal quantities, the first law of thermodynamics is thus expressed as: where δQ and δW are "inexact", i.e. path-dependent, and dU is "exact", i.e. path-independent. Product highlight
OverviewIn general, an inexact differential, as contrasted with an exact differential, of a function f is denoted:
An inexact differential is one whose integral is path dependent. This may be expressed mathematically for a function of two variables as
A differential dQ that is not exact is said to be integrable when there is a function 1/τ such that the new differential dQ/τ is exact. The function 1/τ is called the integrating factor, τ being the integrating denominator. Differentials which are not exact are often denoted with a δ rather than a d. For example, in thermodynamics, δQ and δW denote infinitesimal amounts of heat energy and work, respectively. ExampleAs an example, the use of the inexact differential in thermodynamics is a way to mathematically quantify functions that are not state functions and thus path dependent. In thermodynamic calculations, the use of the symbol ΔQ is a mistake, since heat is not a state function having initial and final values. It would, however, be correct to use lower case δQ in the inexact differential expression for heat. The offending Δ belongs further down in the Thermodynamics section in the equation : is true for constant pressure. See also
References |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Inexact_differential". A list of authors is available in Wikipedia. |


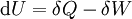



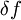
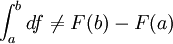 ; as is true of point functions. In fact, F(b) and F(a), in general, are not defined.
; as is true of point functions. In fact, F(b) and F(a), in general, are not defined.
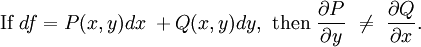
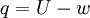 , which should be :
, which should be :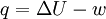 (Baierlein, p. 10, equation 1.11, though he denotes internal energy by
(Baierlein, p. 10, equation 1.11, though he denotes internal energy by