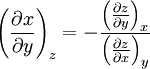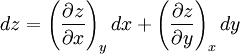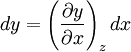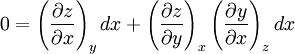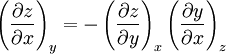To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Triple product ruleThe triple product rule, known variously as the cyclic chain rule, cyclic relation, or Euler's chain rule, is a formula which relates partial derivatives of three interdependent variables. The rule finds application in thermodynamics, where frequently three variables can be related by a function of the form f(x, y, z) = 0, so each variable is given as an implicit function of the other two variables. For example, an equation of state for a fluid relates temperature, pressure, and volume in this manner. The triple product rule for such interrelated variables x, y, and z comes from using a reciprocity relation on the result of the implicit function theorem in two variables and is given by
Product highlightHere the subscripts indicate which variables are held constant when the partial derivative is taken. That is, to explicitly compute the partial derivative of x with respect to y with z held constant, one would write x as a function of y and z and take the partial derivative of this function with respect to y only. The advantage of the triple product rule is that by rearranging terms, one can derive a number of substitution identities which allow one to replace partial derivatives which are difficult to analytically evaluate, experimentally measure, or integrate with quotients of partial derivatives which are easier to work with. For example, Various other forms of the rule are present in the literature; these can be derived by permuting the variables {x, y, z}. DerivationAn informal derivation follows. Suppose that f(x, y, z) = 0. Write z as a function of x and y. Thus the total derivative dz is Suppose that we move along a curve with dz = 0, where the curve is parameterized by x. Thus y can be written in terms of x, so on this curve Therefore the equation for dz = 0 becomes Dividing by dx and rearranging terms gives Dividing by the derivatives on the right hand side gives the triple product rule Note that this proof makes many implicit assumptions regarding the existence of partial derivatives, the existence of the total derivative dz, the ability to construct a curve in some neighborhood with dz = 0, and the nonzero value of partial derivatives and their reciprocals. A formal proof based on mathematical analysis would eliminate these potential ambiguities and grey zones. See also
References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Triple_product_rule". A list of authors is available in Wikipedia. |


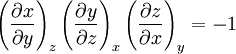 .
.