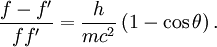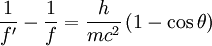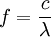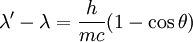To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Compton scattering
In physics, Compton scattering or the Compton effect is the decrease in energy (increase in wavelength) of an X-ray or gamma ray photon, when it interacts with matter. Inverse Compton scattering also exists, where the photon gains energy (decreasing in wavelength) upon interaction with matter. The amount the wavelength increases by is called the Compton shift. Although nuclear compton scattering exists, Compton scattering usually refers to the interaction involving only the electrons of an atom. The Compton effect was observed by Arthur Holly Compton in 1923 and further verified by his graduate student Y. H. Woo in the years following. Arthur Compton earned the 1927 Nobel Prize in Physics for the discovery. The effect is important because it demonstrates that light cannot be explained purely as a wave phenomenon. Thomson scattering, the classical theory of an electromagnetic wave scattered by charged particles, cannot explain any shift in wavelength. Light must behave as if it consists of particles in order to explain the Compton scattering. Compton's experiment convinced physicists that light can behave as a stream of particles whose energy is proportional to the frequency. The interaction between electrons and high energy photons results in the electron being given part of the energy (making it recoil), and a photon containing the remaining energy being emitted in a different direction from the original, so that the overall momentum of the system is conserved. If the photon still has enough energy left, the process may be repeated. If the photon has sufficient energy (in general a few eV, right around the energy of visible light), it can even eject an electron from its host atom entirely (a process known as the Photoelectric effect). Product highlight
The Compton shift formula
Compton used a combination of three fundamental formulas representing the various aspects of classical and modern physics, combining them to describe the quantum behavior of light.
The final result gives us the Compton scattering equation: where
DerivationBegin with energy and momentum conservation:
Solving (1)Now we fill in for the energy part: We solve this for pe': Solving (2)Rearrange equation (2) and square it to see Putting it togetherThen we have two equations for Now, one simplifies. First by multiplying both sides by c2: Next, multiply out the right-hand side: A few terms cancel from both sides, so we have Then divide both sides by ' − 2h' to see Now divide both sides by mc2 and then by Now the left-hand side can be rewritten as simply This is equivalent to the Compton scattering equation, but it is usually written using λs rather than fs. To make that switch use so that finally, ApplicationsCompton scatteringCompton scattering is of prime importance to radiobiology, as it happens to be the most probable interaction of high energy X rays with atomic nuclei in living beings and is applied in radiation therapy. In material physics, Compton scattering can be used to probe the wave function of the electrons in matter in the momentum representation. Compton scattering is an important effect in gamma spectroscopy which gives rise to the Compton edge, as it is possible for the gamma rays to scatter out of the detectors used. Compton suppression is used to detect stray scatter gamma rays to counteract this effect. Inverse Compton scatteringInverse Compton scattering is important in astrophysics. In X-ray astronomy, the accretion disk surrounding a black hole is believed to produce a thermal spectrum. The lower energy photons produced from this spectrum are scattered to higher energies by relativistic electrons in the surrounding corona. This is believed to cause the power law component in the X-ray spectra (0.2-10 keV) of accreting black holes. The effect is also observed when photons from the cosmic microwave background move through the hot gas surrounding a galaxy cluster. The CMB photons are scattered to higher energies by the electrons in this gas, resulting in the Sunyaev-Zel'dovich effect. See also
Categories: Atomic physics | Foundational quantum physics | X-rays | Scattering |
||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Compton_scattering". A list of authors is available in Wikipedia. |





 is the wavelength of the photon before scattering,
is the wavelength of the photon before scattering,
 is the wavelength of the photon after scattering,
is the wavelength of the photon after scattering,
 is the angle by which the photon's heading changes,
is the angle by which the photon's heading changes,
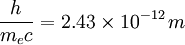 is known as the
is known as the 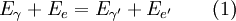
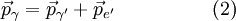
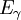 and
and 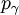 are the energy and momentum of the photon and
are the energy and momentum of the photon and
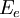 and
and 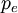 are the energy and momentum of the electron.
are the energy and momentum of the electron.
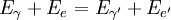
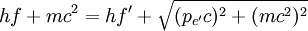
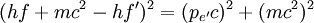
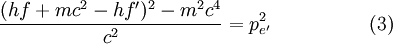
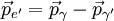
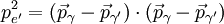
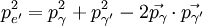
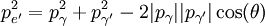
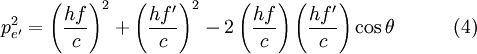
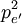 (eq 3 & 4), which we equate:
(eq 3 & 4), which we equate:
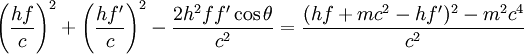
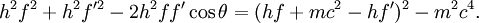
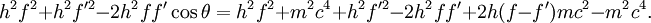
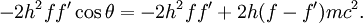
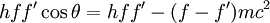
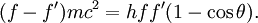
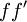 :
: