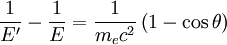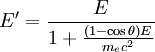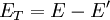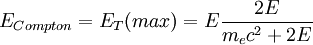My watch list

Compton edge

In spectrophotometry, the Compton edge is a feature of the spectrograph that results from the Compton scattering in the scintillator or detector. When a gamma-ray scatters off the scintillator but escapes, only a fraction of its energy is registered by the detector. This leads to a spectrum of gamma-rays in the data that is not really there. The highest energy that occurs from this process is the Compton edge.

Additional recommended knowledge

How to quickly check pipettes?

Weighing the right way

Guide to balance cleaning: 8 simple steps

Background

In a Compton scattering process, an incident photon collides with an electron in the scintillator. The amount of energy exchanged varies with angle, and is given by the formula:

$\frac{1}{E^\prime} - \frac{1}{E} = \frac{1}{m_e c^2}\left(1-\cos \theta \right)$

or $E^\prime = \frac{E}{1 + \frac{(1 - \cos \theta)E}{m_e c^2}}$

E is the energy of the incident photon.
E' is the energy of the outgoing photon, which escapes the detector.
$m e$ is the mass of the electron.
c is the speed of light.
$θ$ is the angle of deflection for the photon.

The amount of energy transferred to the scintillator varies with the angle of deflection. As $θ$ approaches zero, none of the energy is transferred. The maximum amount of energy is transferred when $θ$ approaches 180 degrees.

$E_T = E - E^\prime$

$E_{Compton} = E_T (max) = E \frac{2E}{m_e c^2 + 2E}$

It is impossible for the photon to transfer any more energy via this process, hence there is a sharp cutoff at this energy giving rise to the name Compton edge.

Compton edge

Additional recommended knowledge

How to quickly check pipettes?

Weighing the right way

Guide to balance cleaning: 8 simple steps

Background

Spectrograph Feature

See also

About chemeurope.com

About LUMITOS

Advertise with LUMITOS