To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Rydberg formulaThe Rydberg formula is used in atomic physics for describing the wavelengths of spectral lines of many chemical elements. The formula was invented by the Swedish physicist Johannes Rydberg and presented on November 5, 1888. Product highlight
HistoryIn the 1880's, Rydberg worked on a formula describing the relation between the wavelengths in spectral lines of alkali metals. He noticed that lines came in series and he found that he could simplify his calculations by using the wavenumber (the number of waves occupying a set unit of length, equal to 1/λ, the inverse of the wavelength) as his unit of measurement. He plotted the wavenumbers of successive lines in each series against consecutive integers which represented the order of the lines in that particular series. Finding that the resulting curves were similarly shaped, he sought a single function which could generate all of them, when appropriate constants were inserted. First he tried the formula: Rydberg was just trying: Rydberg rewrote this in terms of wavenumbers as n = no − 4no/m ². This shows that hydrogen is a special case with m= 0 and C0=4no. Co is a universal constant common to all elements. Now this constant is known as the Rydberg constant, and m is known as the quantum defect. Expressing results in terms of wavenumber, not wavelength, was the key to Rydberg's discovery. The fundamental role of wavenumbers was also emphasized by the Rydberg-Ritz combination principle of 1908. The fundamental reason for this lies in quantum mechanics. Light wavenumber is proportional to frequency (1/λ = frequency/c), and therefore also proportional to light quantum energy E. Thus, 1/λ = E/hc. Modern understanding is that Rydberg's plots were simplified because of the underlying simplicity of the behavior of spectral lines, in terms of fixed (quantized) energy differences between electron orbitals in atoms. This phenomenon was first understood by Niels Bohr in 1913, as incorporated in the Bohr model of the atom. In Bohr's conception of the atom, the integer Rydberg (and Balmer) n numbers represent electron orbitals at different integral distances from the atom. A frequency (or spectral energy) emitted in a transition from n1 to n2 therefore represents the photon energy emitted or absorbed when an electron makes a jump from orbital 1 to orbital 2. Rydberg formula for hydrogenWhere
By setting n1 to 1 and letting n2 run from 2 to infinity, the spectral lines known as the Lyman series converging to 91nm are obtained, in the same manner:
The Lyman series is in the ultraviolet while the Balmer series is in the visible and the Paschen, Brackett, Pfund, and Humphreys series are in the infrared. Rydberg formula for any hydrogen-like elementThe formula above can be extended for use with any hydrogen-like chemical elements. where
It's important to notice that this formula can be applied only to hydrogen-like, also called hydrogenic atoms of chemical elements, i.e. atoms with only one electron being affected by an easy-to-estimate effective nuclear charge. Examples would include He+, Li2+, Be3+ etc., where no other electrons exist in the atom. The Rydberg formula provides correct wavelengths for extremely distant electrons, where the effective nuclear charge can be estimated as the same as that for hydrogen, since all but one of the nuclear charges have been screened by other electrons, and the core of the atom has an effective positive charge of +1. Finally, with certain modifications (replacement of Z by Z-1, and use of the integers 1 and 2 for the n's to give a numerical value of 3/4 for the difference of their inverse squares), the Rydberg formula provides correct values in the special case of K-alpha lines, since the transition in question is the K-alpha transition of the electron from the 1s orbital to the 2p orbital. This is analogous to the Lyman-alpha line transition for hydrogen, and has the same frequency factor. Because the 2p electron is not screened by any other electrons in the atom from the nucleus, the nuclear charge is diminished only by the single remaining 1s electron, causing the system to be effectively a hydrogenic atom, but with a diminished nuclear charge Z-1. Its frequency is thus the Lyman-alpha hydrogen frequency, increased by a factor of (Z-1)2. This formula of f = c/λ = Lyman-alpha frequency * (Z-1)2 is historically known as Moseley's law (having added a factor c to convert wavelength to frequency), and can be used to predict wavelengths of the Kα (K-alpha) X-ray spectral emission lines of chemical elements from aluminum to gold. See the biography of Henry Moseley for the historical importance of this law, which was derived empirically at about the same time it was explained by the Bohr model of the atom. For other spectral transitions in multi-electron atoms, the Rydberg formula generally provides incorrect results, since the magnitude of the screening of inner electrons for outer-electron transitions, is variable and not possible to compensate for in the simple manner above. References
See alsoCategories: Atomic physics | Foundational quantum physics | Hydrogen physics |
|||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Rydberg_formula". A list of authors is available in Wikipedia. |





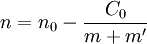 , where n is the line's wavenumber, n0 is the series limit, m is the line's ordinal number in the series, m' is a constant different for different series and C0 is a universal constant. This did not work very well.
, where n is the line's wavenumber, n0 is the series limit, m is the line's ordinal number in the series, m' is a constant different for different series and C0 is a universal constant. This did not work very well.
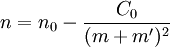 when he saw Balmer's formula for the hydrogen spectrum λ=hm ²/(m ² − 4).
when he saw Balmer's formula for the hydrogen spectrum λ=hm ²/(m ² − 4).
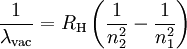
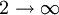
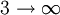
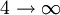
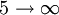
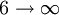
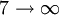
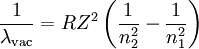
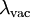 is the wavelength of the light emitted in vacuum;
is the wavelength of the light emitted in vacuum;
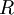 is the
is the 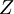 is the
is the 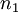 and
and 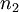 are integers such that
are integers such that 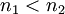 .
.


