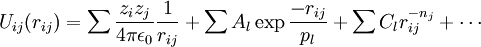To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Molecular dynamicsMolecular dynamics (MD) is a form of computer simulation wherein atoms and molecules are allowed to interact for a period of time under known laws of physics, giving a view of the motion of the atoms. Because molecular systems generally consist of a vast number of particles, it is impossible to find the properties of such complex systems analytically; MD simulation circumvents this problem by using numerical methods. It represents an interface between laboratory experiments and theory, and can be understood as a "virtual experiment".
Although it has been known since Boltzmann's discoveries in the 19th century that matter consists of interacting particles in motion, many people still think of molecules as rigid museum models. Richard Feynman said in 1963 that "everything that living things do can be understood in terms of the jiggling and wiggling of atoms."[1] One of MD's key contributions is creating awareness that molecules like proteins and DNA are machines in motion.[2] MD probes the relationship between molecular structure, movement and function. Molecular dynamics is a multidisciplinary method. Its laws and theories stem from mathematics, physics, and chemistry, and it employs algorithms from computer science and information theory. It was originally conceived within theoretical physics in the late 1950's[3], but is applied today mostly in materials science and biomolecules. Before it became possible to simulate molecular dynamics with computers, some undertook the hard work of trying it with physical models such as macroscopic spheres. The idea was to arrange them to replicate the properties of a liquid. J.D. Bernal said, in 1962: "... I took a number of rubber balls and stuck them together with rods of a selection of different lengths ranging from 2.75 to 4 inches. I tried to do this in the first place as casually as possible, working in my own office, being interrupted every five minutes or so and not remembering what I had done before the interruption."[4] Fortunately, now computers keep track of bonds during a simulation. Molecular dynamics is a specialized discipline of molecular modeling and computer simulation based on statistical mechanics; the main justification of the MD method is that statistical ensemble averages are equal to time averages of the system, known as the ergodic hypothesis. MD has also been termed "statistical mechanics by numbers" and "Laplace's vision of Newtonian mechanics" of predicting the future by animating nature's forces[5][6] and allowing insight into molecular motion on an atomic scale. However, long MD simulations are mathematically ill-conditioned, generating cumulative errors in numerical integration that can be minimized with proper selection of algorithms and parameters, but not eliminated entirely. Furthermore, current potential functions are, in many cases, not sufficiently accurate to reproduce the dynamics of molecular systems, so the much more demanding Ab Initio Molecular Dynamics method must be used. Nevertheless, molecular dynamics techniques allow detailed time and space resolution into representative behavior in phase space.
Product highlight
Areas of ApplicationThere is a significant difference between the focus and methods used by chemists and physicists, and this is reflected in differences in the jargon used by the different fields. In chemistry and biophysics, the interaction between the particles is either described by a "force field" (classical MD), a quantum chemical model, or a mix between the two. These terms are not used in physics, where the interactions are usually described by the name of the theory or approximation being used and called the potential energy, or just "potential". Beginning in theoretical physics, the method of MD gained popularity in materials science and since the 1970s also in biochemistry and biophysics. In chemistry, MD serves as an important tool in protein structure determination and refinement using experimental tools such as X-ray crystallography and NMR. It has also been applied with limited success as a method of refining protein structure predictions. In physics, MD is used to examine the dynamics of atomic-level phenomena that cannot be observed directly, such as thin film growth and ion-subplantation. It is also used to examine the physical properties of nanotechnological devices that have not or cannot yet be created. In applied mathematics and theoretical physics, molecular dynamics is a part of the research realm of dynamical systems, ergodic theory and statistical mechanics in general. The concepts of energy conservation and molecular entropy come from thermodynamics. Some techniques to calculate conformational entropy such as principal components analysis come from information theory. Mathematical techniques such as the transfer operator become applicable when MD is seen as a Markov chain. Also, there is a large community of mathematicians working on volume preserving, symplectic integrators for more computationally efficient MD simulations. MD can also be seen as a special case of the discrete element method (DEM) in which the particles have spherical shape (e.g. with the size of their van der Waals radii.) Some authors in the DEM community employ the term MD rather loosely, even when their simulations do not model actual molecules. Design ConstraintsDesign of a molecular dynamics simulation should account for the available computational power. Simulation size (n=number of particles), timestep and total time duration must be selected so that the calculation can finish within a reasonable time period. However, the simulations should be long enough to be relevant to the time scales of the natural processes being studied. To make statistically valid conclusions from the simulations, the time span simulated should match the kinetics of the natural process. Otherwise, it is analogous to making conclusions about how a human walks from less than one footstep. Most scientific publications about the dynamics of proteins and DNA use data from simulations spanning nanoseconds (1E-9 s) to microseconds (1E-6 s). To obtain these simulations, several CPU-days to CPU-years are needed. Parallel algorithms allow the load to be distributed among CPUs; an example is the spatial decomposition in LAMMPS. During a classical MD simulation, the most CPU intensive task is the evaluation of the potential (force field) as a function of the particles' internal coordinates. Within that energy evaluation, the most expensive one is the non-bonded or non-covalent part. In Big O notation, common molecular dynamics simulations scale by O(n2) if all pair-wise electrostatic and van der Waals interactions must be accounted for explicitly. This computational cost can be reduced by employing electrostatics methods such as Particle Mesh Ewald ( O(nlog(n)) ) or good spherical cutoff techniques ( O(n) ). Another factor that impacts total CPU time required by a simulation is the size of the integration timestep. This is the time length between evaluations of the potential. The timestep must be chosen small enough to avoid discretization errors (i.e. smaller than the fastest vibrational frequency in the system). Typical timesteps for classical MD are in the order of 1 femtosecond (1E-15 s). This value may be extended by using algorithms such as SHAKE, which fix the vibrations of the fastest atoms (e.g. hydrogens) into place. Multiple time scale methods have also been developed, which allow for extended times between updates of slower long-range forces.[7][8][9] For simulating molecules in a solvent, a choice should be made between explicit solvent and implicit solvent. Explicit solvent particles (such as the TIP3P and SPC/E water models) must be calculated expensively by the force field, while implicit solvents use a mean-field approach. The impact of explicit solvents on CPU-time can be 10-fold or more. But the granularity and viscosity of explicit solvent is essential to reproduce certain properties of the solute molecules. In all kinds of molecular dynamics simulations, the simulation box size must be large enough to avoid boundary condition artifacts. Boundary conditions are often treated by choosing fixed values at the edges, or by employing periodic boundary conditions in which one side of the simulation loops back to the opposite side, mimicking a bulk phase. Microcanonical ensemble (NVE)In the microcanonical, or NVE ensemble, the system is isolated from changes in moles (N), volume (V) and energy (E). It corresponds to an adiabatic process with no heat exchange. A microcanonical molecular dynamics trajectory may be seen as an exchange of potential and kinetic energy, with total energy being conserved. For a system of N particles with coordinates X and velocities V, the following pair of first order differential equations may be written in Newton's notation as The potential energy function U(X) of the system is a function of the particle coordinates X. It is referred to simply as the "potential" in Physics, or the "force field" in Chemistry. The first equation comes from Newton's laws; the force F acting on each particle in the system can be calculated as the negative gradient of U(X). For every timestep, each particle's position X and velocity V may be integrated with a symplectic method such as Verlet. The time evolution of X and V is called a trajectory. Given the initial positions (e.g. from theoretical knowledge) and velocities (e.g. randomized Gaussian), we can calculate all future (or past) positions and velocities. One frequent source of confusion is the meaning of temperature in MD. Commonly we have experience with macroscopic temperatures, which involve a huge number of particles. But temperature is a statistical quantity. If there is a large enough number of atoms, statistical temperature can be estimated from the instantaneous temperature, which is found by equating the kinetic energy of the system to nkBT/2 where n is the number of degrees of freedom of the system. A temperature-related phenomenon arises due to the small number of atoms that are used in MD simulations. For example, consider simulating the growth of a copper film starting with a substrate containing 500 atoms and a deposition energy of 100 eV. In the real world, the 100 eV from the deposited atom would rapidly be transported through and shared among a large number of atoms (1010 or more) with no big change in temperature. When there are only 500 atoms, however, the substrate is almost immediately vaporized by the deposition. Something similar happens in biophysical simulations. The temperature of the system in NVE is naturally raised when macromolecules such as proteins undergo exothermic conformational changes and binding. Canonical ensemble (NVT)In the canonical ensemble, moles (N), volume (V) and temperature (T) are conserved. It is also sometimes called constant temperature molecular dynamics (CTMD). In NVT, the energy of endothermic and exothermic processes is exchanged with a thermostat. A variety of thermostat methods are available to add and remove energy from the boundaries of an MD system in a realistic way, approximating the canonical ensemble. Popular techniques to control temperature include the Nosé-Hoover thermostat and Langevin dynamics. Isothermal-Isobaric (NPT) ensembleIn the isothermal-isobaric ensemble, moles (N), pressure (P) and temperature (T) are conserved. In addition to a thermostat, a barostat is needed. It corresponds most closely to laboratory conditions with a flask open to ambient temperature and pressure. In the simulation of biological membranes, isotropic pressure control is not appropriate. For lipid bilayers, pressure control occurs under constant membrane area (NPAT) or constant surface tension "gamma" (NPγT). Generalized ensemblesThe replica exchange method is a generalized ensemble. It was originally created to deal with the slow dynamics of disordered spin systems. It is also called parallel tempering. The replica exchange MD (REMD) formulation [10] tries to overcome the multiple-minima problem by exchanging the temperature of non-interacting replicas of the system running at several temperatures. Potentials in MD simulationsMain Article: Force field A molecular dynamics simulation requires the definition of a potential function, or a description of the terms by which the particles in the simulation will interact. In chemistry and biology this is usually referred to as a force field. Potentials may be defined at many levels of physical accuracy; those most commonly used in chemistry are based on molecular mechanics and embody a classical treatment of particle-particle interactions that can reproduce structural and conformational changes but usually cannot reproduce chemical reactions. The reduction from a fully quantum description to a classical potential entails two main approximations. The first one is the Born-Oppenheimer approximation, which states that the dynamics of electrons is so fast that they can be considered to react instantaneously to the motion of their nuclei. As a consequence, they may be treated separately. The second one treats the nuclei, which are much heavier than electrons, as point particles that follow classical Newtonian dynamics. In classical molecular dynamics the effect of the electrons is approximated as a single potential energy surface, usually representing the ground state. When finer levels of detail are required, potentials based on quantum mechanics are used; some techniques attempt to create hybrid classical/quantum potentials where the bulk of the system is treated classically but a small region is treated as a quantum system, usually undergoing a chemical transformation. Empirical potentialsEmpirical potentials used in chemistry are frequently called force fields, while those used in materials physics are called just empirical or analytical potentials. Most force fields in chemistry are empirical and consist of a summation of bonded forces associated with chemical bonds, bond angles, and bond dihedrals, and non-bonded forces associated with van der Waals forces and electrostatic charge. Empirical potentials represent quantum-mechanical effects in a limited way through ad-hoc functional approximations. These potentials contain free parameters such as atomic charge, van der Waals parameters reflecting estimates of atomic radius, and equilibrium bond length, angle, and dihedral; these are obtained by fitting against detailed electronic calculations (quantum chemical simulations) or experimental physical properties such as elastic constants, lattice parameters and spectroscopic measurements. Because of the non-local nature of non-bonded interactions, they involve at least weak interactions between all particles in the system. Its calculation is normally the bottleneck in the speed of MD simulations. To lower the computational cost, force fields employ numerical approximations such as shifted cutoff radii, reaction field algorithms, particle mesh Ewald summation, or the newer Particle-Particle Particle Mesh (P3M). Chemistry force fields commonly employ preset bonding arrangements (an exception being ab-initio dynamics), and thus are unable to model the process of chemical bond breaking and reactions explicitly. On the other hand, many of the potentials used in physics, such as those based on the bond order formalism can describe several different coordinations of a system and bond breaking. Examples of such potentials include the Brenner potential[11] for hydrocarbons and its further developments for the C-Si-H and C-O-H systems. The ReaxFF potential[12] can be considered a fully reactive hybrid between bond order potentials and chemistry force fields. Pair potentials vs. many-body potentialsThe potential functions representing the non-bonded energy are formulated as a sum over interactions between the particles of the system. The simplest choice, employed in many popular force fields, is the "pair potential", in which the total potential energy can be calculated from the sum of energy contributions between pairs of atoms. An example of such a pair potential is the non-bonded Lennard-Jones potential (also known as the 6-12 potential), used for calculating van der Waals forces. Another example is the Born (ionic) model of the ionic lattice. The first term in the next equation is Coulomb's law for a pair of ions, the second term is the short-range repulsion explained by Pauli's exclusion principle and the final term is the dispersion interaction term. Usually, a simulation only includes the dipolar term, although sometimes the quadrupolar term is included as well. In many-body potentials, the potential energy includes the effects of three or more particles interacting with each other. In simulations with pairwise potentials, global interactions in the system also exist, but they occur only through pairwise terms. In many-body potentials, the potential energy cannot be found by a sum over pairs of atoms, as these interactions are calculated explicitly as a combination of higher-order terms. In the statistical view, the dependency between the variables cannot in general be expressed using only pairwise products of the degrees of freedom. For example, the Tersoff potential[13], which was originally used to simulate carbon, silicon and germanium and has since been used for a wide range of other materials, involves a sum over groups of three atoms, with the angles between the atoms being an important factor in the potential. Other examples are the embedded-atom method (EAM)[14] and the Tight-Binding Second Moment Approximation (TBSMA) potentials[15], where the electron density of states in the region of an atom is calculated from a sum of contributions from surrounding atoms, and the potential energy contribution is then a function of this sum. Semi-empirical potentialsSemi-empirical potentials make use of the matrix representation from quantum mechanics. However, the values of the matrix elements are found through empirical formulae that estimate the degree of overlap of specific atomic orbitals. The matrix is then diagonalized to determine the occupancy of the different atomic orbitals, and empirical formulae are used once again to determine the energy contributions of the orbitals. There are a wide variety of semi-empirical potentials, known as tight-binding potentials, which vary according to the atoms being modeled. Polarizable potentialsMain article: Force field Most classical force fields implicitly include the effect of polarizability, e.g. by scaling up the partial charges obtained from quantum chemical calculations. These partial charges are stationary with respect to the mass of the atom. But molecular dynamics simulations can explicitly model polarizability with the introduction of induced dipoles through different methods, such as Drude particles or fluctuating charges. This allows for a dynamic redistribution of charge between atoms which responds to the local chemical environment. For many years, polarizable MD simulations have been touted as the next generation. For homogenous liquids such as water, increased accuracy has been achieved through the inclusion of polarizability[16]. Some promising results have also been achieved for proteins[17]. However, it is still uncertain how to best approximate polarizability in a simulation. Ab-initio methodsIn classical molecular dynamics, a single potential energy surface (usually the ground state) is represented in the force field. This is a consequence of the Born-Oppenheimer approximation. If excited states, chemical reactions or a more accurate representation is needed, electronic behavior can be obtained from first principles by using a quantum chemical method, such as [Density Functional Theory]. This is known as Ab Initio Molecular Dynamics (AIMD). Due to the cost of treating the electronic degrees of freedom, the computational cost of this simulations is much higher than classical molecular dynamics. This implies that AIMD is limited to smaller systems and shorter periods of time. Ab-initio quantum-mechanical methods may be used to calculate the potential energy of a system on the fly, as needed for conformations in a trajectory. This calculation is usually made in the close neighborhood of the reaction coordinate. Although various approximations may be used, these are based on theoretical considerations, not on empirical fitting. Ab-Initio calculations produce a vast amount of information that is not available from empirical methods, such as density of electronic states. A significant advantage of using ab-initio methods is the ability to study reactions that involve breaking or formation of covalent bonds, which correspond to multiple electronic states. A popular software for ab-initio molecular dynamics is the Car-Parrinello Molecular Dynamics (CPMD) package based on the density functional theory. Hybrid QM/MMQM (quantum-mechanical) methods are very powerful however they are computationally expensive, while the MM (classical or molecular mechanics) methods are fast but suffer from several limitations (require extensive parameterization; energy estimates obtained are not very accurate; cannot be used to simulate reactions where covalent bonds are broken/formed; and are limited in their abilities for providing accurate details regarding the chemical environment). A new class of method has emerged that combines the good points of QM (accuracy) and MM (speed) calculations. These methods are known as mixed or hybrid quantum-mechanical and molecular mechanics methods (hybrid QM/MM). The methodology for such techniques was introduced by Warshel and coworkers. In the recent years have been pioneered by several groups including: Arieh Warshel (University of Southern California), Weitao Yang (Duke University), Sharon Hammes-Schiffer (The Pennsylvania State University), Donald Truhlar and Jiali Gao (University of Minnesota) and Kenneth Merz (University of Florida). The most important advantage of hybrid QM/MM methods is the speed. The cost of doing classical molecular dynamics (MM) in the most straightforward case scales O(n2), where N is the number of atoms in the system. This is mainly due to electrostatic interactions term (every particle interacts with every other particle). However, use of cutoff radius, periodic pair-list updates and more recently the variations of the particle-mesh Ewald's (PME) method has reduced this between O(N) to O(n2). In other words, if a system with twice many atoms is simulated then it would take between twice to four times as much computing power. On the other hand the simplest ab-initio calculations typically scale O(n3) or worse (Restricted Hartree-Fock calculations have been suggested to scale ~O(n2.7)). To overcome the limitation, a small part of the system is treated quantum-mechanically (typically active-site of an enzyme) and the remaining system is treated classically. In more sophisticated implementations, QM/MM methods exist to treat both light nuclei susceptible to quantum effects (such as hydrogens) and electronic states. This allows generation of hydrogen wave-functions (similar to electronic wave-functions). This methodology has been useful in investigating phenomenon such as hydrogen tunneling. One example where QM/MM methods have provided new discoveries is the calculation of hydride transfer in the enzyme liver alcohol dehydrogenase. In this case, tunneling is important for the hydrogen, as it determines the reaction rate.[18] Coarse-graining and reduced representationsAt the other end of the detail scale are coarse-grained and lattice models. Instead of explicitly representing every atom of the system, one uses "pseudo-atoms" to represent groups of atoms. MD simulations on very large systems may require such large computer resources that they cannot easily be studied by traditional all-atom methods. Similarly, simulations of processes on long timescales (beyond about 1 microsecond) are prohibitively expensive, because they require so many timesteps. In these cases, one can sometimes tackle the problem by using reduced representations, which are also called coarse-grained models. Examples for coarse graining (CG) methods are discontinuous molecular dynamics (CG-DMD)[19] and Go-models[20]. Coarse-graining is done sometimes taking larger pseudo-atoms. Such united atom approximations have been used in MD simulations of biological membranes. The aliphatic tails of lipids are represented by a few pseudo-atoms by gathering 2-4 methylene groups into each pseudo-atom. The parameterization of these very coarse-grained models must be done empirically, by matching the behavior of the model to appropriate experimental data or all-atom simulations. Ideally, these parameters should account for both enthalpic and entropic contributions to free energy in an implicit way. When coarse-graining is done at higher levels, the accuracy of the dynamic description may be less reliable. But very coarse-grained models have been used successfully to examine a wide range of questions in structural biology. Examples of applications of coarse-graining in biophysics:
The simplest form of coarse-graining is the "united atom" (sometimes called "extended atom") and was used in most early MD simulations of proteins, lipids and nucleic acids. For example, instead of treating all four atoms of a CH3 methyl group explicitly (or all three atoms of CH2 methylene group), one represents the whole group with a single pseudo-atom. This pseudo-atom must, of course, be properly parameterized so that its van der Waals interactions with other groups have the proper distance-dependence. Similar considerations apply to the bonds, angles, and torsions in which the pseudo-atom participates. In this kind of united atom representation, one typically eliminates all explicit hydrogen atoms except those that have the capability to participate in hydrogen bonds ("polar hydrogens"). An example of this is the Charmm 19 force-field. The polar hydrogens are usually retained in the model, because proper treatment of hydrogen bonds requires a reasonably accurate description of the directionality and the electrostatic interactions between the donor and acceptor groups. A hydroxyl group, for example, can be both a hydrogen bond donor and a hydrogen bond acceptor, and it would be impossible to treat this with a single OH pseudo-atom. Note that about half the atoms in a protein or nucleic acid are nonpolar hydrogens, so the use of united atoms can provide a substantial savings in computer time. Examples of applicationsMolecular dynamics is used in many fields of science.
The following two biophysical examples are not run-of-the-mill MD simulations. They illustrate almost heroic efforts to produce simulations of a system of very large size (a complete virus) and very long simulation times (500 microseconds):
Molecular dynamics algorithmsIntegrators
Short-range interaction algorithms
Long-range interaction algorithms
Parallelization strategies
Major software for MD simulations
Related software
See also
References
General references
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Molecular_dynamics". A list of authors is available in Wikipedia. |





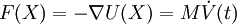
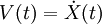
![U(r) = 4\varepsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^{6} \right]](images/math/1/8/8/1883782f03e940f640cd936f6f68adc3.png)