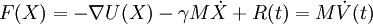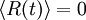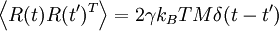Langevin dynamics

Langevin dynamics is an approach to mechanics using simplified models and using stochastic differential equations to account for omitted degrees of freedom. A molecular system in the real world is unlikely to be present in vacuum. Jostling of solvent or air molecules causes friction, and the occasional high velocity collision will perturb the system. Langevin dynamics attempts to extend molecular dynamics to allow for these effects. Also, Langevin dynamics allow controlling the temperature like a thermostat, thus approximating the canonical ensemble.

Additional recommended knowledge

Correct Test Weight Handling Guide: 12 Practical Tips

Weighing the right way

How to quickly check pipettes?

Langevin dynamics mimic the viscous aspect of a solvent. In itself, it is not a complete implicit solvent, i.e. it does not account for either the electrostatic screening nor the hydrophobic effect. For a system of N particles with masses M, coordinates X and velocities V, the continuous form of the simplest Langevin equation is ^[1]

Where F(X) is the force felt by the particles, U(X) is the potential energy (e.g., the force field), γ is the collision parameter or damping constant (reciprocal time units).

R(t) is a random force vector, which is a stationary Gaussian process with zero-mean:

Where T is the target temperature, k_B is Boltzmann's constant, and δ is the Dirac delta.

If the main objective is to control temperature, care should be exercised to use a small damping constant γ. As γ grows, it spans the inertial all the way to the diffusive (Brownian) regime. The Langevin dynamics limit of non-inertia is commonly described as Brownian dynamics.

Langevin differential equations which govern a random variable X can be reformulated as "Fokker-Planck" differential equations (Fokker-Planck Eq'n), or "master equations," which govern the probability distribution of X.

References

1. ^ Schlick, Tamar (2002). Molecular Modeling and Simulation. Springer, 435-438. ISBN 0-387-95404-X. 

See also

• Hamiltonian mechanics
• Molecular dynamics
• Brownian dynamics
• Statistical mechanics
• Implicit solvation
• stochastic differential equations

External links

• Langevin Dynamics (LD) Simulation