My watch list
my.chemeurope.com  

my.chemeurope.com

With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.

  • My watch list
  • My saved searches
  • My saved topics
  • My newsletter
Register free of charge
Login  
eng  
DeutschEnglishFrançaisEspañol

Poisson-Boltzmann equation



The Poisson-Boltzmann equation is a differential equation that describes electrostatic interactions between molecules in ionic solutions. It is the mathematical base for the Gouy-Chapman Double layer (interfacial) theory; first proposed by Gouy in 1910 and complemented by Chapman in 1913. The equation is important in the fields of molecular dynamics and biophysics because it can be used in modeling implicit solvation, an approximation of the effects of solvent on the structures and interactions of proteins, DNA, RNA, and other molecules in solutions of different ionic strength. It is often difficult to solve the Poisson-Boltzmann equation for complex systems, but several computer programs have been created to solve it numerically.

The equation can be written as:

\vec{\nabla}\left[\epsilon(\vec{r})\vec{\nabla}\Psi(\vec{r})\right] = -4\pi\rho^{f}(\vec{r}) - 4\pi\sum_{i}c_{i}^{\infty}z_{i}\lambda(\vec{r})qe^{\frac{-z_{i}q\Psi(\vec{r})}{k_B T}}

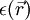where \epsilon(\vec{r}) represents the position-dependent dielectric, 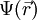\Psi(\vec{r}) represents the electrostatic potential, 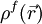\rho^{f}(\vec{r}) represents the charge density of the solute, 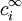c_{i}^{\infty} represents the concentration of the ion i at a distance of infinity from the solute, 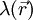zi is the charge of the ion, q is the charge of a proton, kB is the Boltzmann constant, T is the temperature, and \lambda(\vec{r}) is a factor for the position-dependent accessibility of position r to the ions in solution. If the potential is not large, the equation can be linearized to be solved more efficiently.[1][2][3]

References

  1. ^ Fogolari F, Brigo A, Molinari H. (2002). The Poisson-Boltzmann equation for biomolecular electrostatics: a tool for structural biology. J Mol Recognit 15(6):377-92. (See this paper for derivation.)
  2. ^ G.L. Gouy, j. de phys 9, 457 (1910)
  3. ^ D.L. Chapman, Philos. Mag. 25, 475 (1913)

See also

  • DelPhi: a canonical finite difference Poisson-Boltzmann solver for protein, now distributed as free software


 
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Poisson-Boltzmann_equation". A list of authors is available in Wikipedia.
Your browser is not current. Microsoft Internet Explorer 6.0 does not support some functions on Chemie.DE