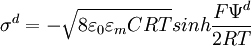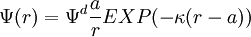To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Double layer (interfacial)
DL is usually important for systems with high surface area. This might be colloids with very small sizes, on the scale of a micrometer or even nanometers. Porous bodies with small size of pores on the same scale is another example.
There are many phenomena that exist due to Double Layer. One of the most known is electrophoresis. It belongs to a wider group of electrokinetic phenomena. Another group comprises electroacoustic phenomena. Product highlight
HistoryThe earliest model of the electrical double layer is usually attributed to Helmholtz [1] . Helmholtz treated the double layer mathematically as a simple capacitor, based on a physical model in which a single layer of ions is adsorbed at the surface. Later Louis Georges Gouy [2], and David Leonard Chapman [3] made significant improvements by introducing a diffuse model of the electrical double layer, in which the electric potential decreases exponentially away from the surface to the fluid bulk. Gouy-Chapman model fails for highly charged DLs. In order to resolve this problem Stern suggested introduction of additional internal layer, that is now called the Stern layer[4]. Combined Gouy-Chapman-Stern model is most commonly used. It still has some limitations, such as
There are more recent theoretical developments studying these limitations of the Gouy-Chapman-Stern model. They are reviwed by J.Lyklema in "Fundamentals of Interface and Colloid Science" [5], Detailed Description of DLThere are detailed descriptions of the interfacial Double Layer in many books on Colloid and Interface Science[6], [7], [8],[9],[10], [11]. There is an IUPAC Technical Report [12] prepared by a group of most known world experts on the subject of interfacial Double Layer and related electrokinetic phenomena.
The diffuse layer, or at least part of it, can move under the influence of tangential stress. There is a conventionally introduced slipping plane that separates mobile fluid from fluid that remains attached to the surface. Electric potential at this plane is called electrokinetic potential or zeta potential. It is also denoted as ζ-potential. Electric potential on the external boundary of the Stern layer is referred to as Stern potential. Electric potential at the surface is electric surface potential. Usually zeta potential is used for estimating the degree of DL charge. A characteristic value of this electric potential in the DL is 25 mV with a maximum value around 100 mV. Chemical composition of the sample that brings ζ-potential down to 0 is called iso-electric point. It is usually certain pH value. Zeta potential can be measured using electrophoresis or electroacoustic phenomena. The characteristic thickness of the Double Layer is Debye length κ-1. It is reciprocally proportional to the square root of the ion concentration C. In aqueous solution it is on scale of a few nanometers. The theory for a flat surface and a symmetrical electrolyte has been given by Gouy and Chapman, ref.1. It is usually referred to as Gouy-Chapman theory. It yields a simple relationship between electric charge in the diffuse layer σd and the Stern potential Ψd: There is no general analytical solution for mixed electrolytes, curved surfaces or even spherical particles. There is an asymptotic solution for spherical particles with low charged DLs. In the case when electric potential over DL is less than 25 mV, the so-called Debye-Huckel approximation holds. It yields the following expression for electric potential Ψ in the spherical DL as a function of the distance r from the particle center: There are several important asymptotic models which play important roles in theoretical developments associated with interfacial DL. The first one is "thin Double Layer", Ref.1-7. This model assumes that Double Layer is much thinner than the particle or capillary radius. This restricts the value of the Debye legth and particle radius as following:
This model offers tremendous simplifications for many theories. Theory of electrophoresis is just one example, Ref.2. Theory of Electroacoustic phenomena Ref.6 is another example. The Model of thin Double Layer is valid for most aqueous systems because the Debye length is only a few nanometers there. It breaks only for nano-colloids in solution with ionic strength close to water. The opposite model of "thick Double Layer" assumes that Debye length is larger than particle radius:
This model can be useful for some nano-colloids and non-polar fluids, where Debye length is much larger. The last model introduces "overlapped Double Layers", Ref.6. This is important in concentrated dispersions and emulsions when distances between particles become comparable with Debye length. References
CategoryCategories: Chemical mixtures | Colloidal chemistry | Condensed matter physics | Soft matter |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Double_layer_(interfacial)". A list of authors is available in Wikipedia. |