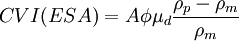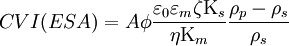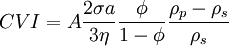Electroacoustic phenomena

Electroacoustic phenomena arises when ultrasound propagates through a fluid containing ions. It moves these ions. This motion generates electric signals because ions have electric charge. This coupling between ultrasound and electric field is called electroacoustic phenomena. Fluid might be a simple Newtonian liquid, or complex heterogeneous dispersion, emulsion or even a porous body. There are several different electroacoustic effects depending on the nature of the fluid.

• Ion Vibration Current/Potential (IVI), an electric signal that arises when an acoustic wave propagates through a homogeneous fluid.
• Streaming Vibration Current/Potential (SVI), an electric signal that arises when an acoustic wave propagates through a porous body in which the pores are filled with fluid.
• Colloid Vibration Current /Potential (CVI), an electric signal that arises when ultrasound propagates through a heterogeneous fluid, such as a dispersion or emulsion.
• Electric Sonic Amplitude (ESA), the inverse of CVI effect, in which an acoustic field arises when an electric field propagates through a heterogeneous fluids.

Additional recommended knowledge

Guide to balance cleaning: 8 simple steps

How to ensure accurate weighing results every day?

Safe Weighing Range Ensures Accurate Results

Ion Vibration Current

Historically, the IVI is the first known electroacoustic effect. It was predicted by Debye in 1933^[1]. He pointed out that the difference in the effective mass or friction coefficient between anion and cation would result in different displacement amplitudes in a longitudinal wave. This difference creates an alternating electric potential between various points in sound wave. This effect was extensively used in 1950’s and 1960’s for characterizing ion solvation. These works are mostly associated with names of Zana ans Yaeger, who published a review of their studies in 1982^[2].

Streaming Vibration Current

Streaming Vibration Current was experimentally observed in 1948 by Williams ^[3]. A theoretical model was developed some 30 years later by Dukhin and oth.^[4]. This effect opens another possibility for characterizing the electric properties of the surfaces in porous bodies.

Collod Vibration Potential / Current

Colloid Vibration Potential/Current was first reported by Hermans and then independently by Rutgers in 1938. It is widely used for characterizing the ζ-potential of various dispersions and emulsions. The effect, theory, experimental verification and multiple applications are discussed in the book by Dukhin and Goetz.^[5]

ElectricSonic Amplitude

Electric Sonic Amplitude was experimentally discovered by Cannon with co-authors in early 1980’s.^[6] It is also widely used for characterizing ζ-potential in dispersions and emulsions. There is review of this effect theory, experimental verification and multiple applications published by Hunter.^[7]

Theory of CVI and ESA

With regard to the theory of CVI and ESA, there was important observation made by O’Brien,^[8] who linked these measured parameters with dynamic electrophoretic mobility μ_d.

where

A is calibration constant, depending on frequency, but not particles properties;

ρ_p is particle density,

ρ_m density of the fluid,

φ is volume fraction of dispersed phase,

Dynamic electrophoretic mobility is similar to electrophoretic mobility that appears in electrophoresis theory. They are identical at low frequencies and/or for sufficiently small particles.

There are several theories of the dynamic electrophoretic mobility. Their overview is given in the Ref.5. Two of them are the most important.

The first one corresponds to Smoluchowski limit. It yields following simple expression for CVI for sufficiently small particles with negligible CVI frequency dependence:

where:

ε₀ is vacuum dielectric permittivity,

ε_m is fluid dielectric permittivity,

ζ is electrokinetic potential

η is dynamic viscosity of the fluid,

K_s is conductivity of the system,

K_m is conductivity of the fluid,

ρ_s is density of the system.

This remarkably simple equation has same wide range of applicability as Smoluchowski equation for electrophoresis. It is independent on shape of the particles, their concentration.

Validity of this equation is restricted with the following two requirements.

First of all it is valid only for thin Double Layer, when Debye length is much smaller than particles radius a:

κa > > 1

Secondly, it neglect contribution of the surface conductivity. This assumes small Dukhin number:

Du < < 1

Restriction of the thin Double Layer limits applicability of this Smoluchwski type theory only to aqueous systems with sufficiently large particles and not very low ionic strength. This thery does not work well for nano-colloids, including proteins and polymers at low ionic strength. It is not valid for low- or non-polar fluids.

There is another theory that is applicable for other extreme case of thick Double Layer, when

κa < 1

This theory takes into consideration overpap of Double Layer that inevitably occur for concentrated systems with thick Double Layer. This allows introduction of so-called "quasi-homogeneous" approach, when overlapped diffuse layers of particles cover complete inter particle space. Theory becomes much simplified in this extreme case, as shown by Shilov and oth. ^[9]. Their derivation predict that surface charge density σ is better parameter than ζ-potential for characterizing electroscoustic phenomena in such systems. Expression for CVI simplified for small particles follows:

There is much more detail description of theory, experiment, modern instruments given in the Ref.5 and shown below external web site.

References

Category

Interface and Colloid Science