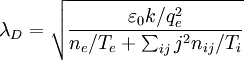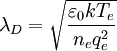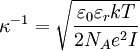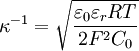Debye length

The notion of Debye length plays an important role in plasma physics, electrolytes and colloids (DLVO theory).

Additional recommended knowledge

What is the Sensitivity of my Balance?

How to quickly check pipettes?

Better weighing performance in 6 easy steps

In plasma physics, the Debye length, named after the Dutch physical chemist Peter Debye, is the scale over which mobile charge carriers (e.g. electrons) screen out electric fields in plasmas and other conductors. In other words, the Debye length is the distance over which significant charge separation can occur. A Debye sphere is a volume whose radius is the Debye length, in which there is a sphere of influence, and outside of which charges are screened.

In space plasmas where the electron density is relatively low, the Debye length may reach macroscopic values, such as in the magnetosphere, solar wind, interstellar medium and intergalactic medium (see table):

Hannes Alfven pointed out that: "In a low density plasma, localized space charge regions may build up large potential drops over distances of the order of some tens of the Debye lengths. Such regions have been called electric double layers. An electric double layer is the simplest space charge distribution that gives a potential drop in the layer and a vanishing electric field on each side of the layer. In the laboratory, double layers have been studied for half a century, but their importance in cosmic plasmas has not been generally recognized.".

Debye length in a plasma

In a plasma, the Debye length is

where

λ_D is the Debye length,

ε₀ is the permittivity of free space,

k is Boltzmann's constant,

q_e is the charge on an electron,

T_e and T_i are the temperatures of the electrons and ions, respectively,

n_e is the density of electrons,

n_ij'is the density of atomic species i, with positive ionic charge jq_e

The ion term is often dropped, giving

although this is only valid when the ions are much colder than the electrons.

Debye length in an electrolyte

In an electrolyte or a colloidal dispersion, the Debye length is usually denoted with symbol κ^-1

where

I is the ionic strength of the electrolyte,

ε₀ is the permittivity of free space,

ε_r is the dielectric constant,

k is the Boltzmann's constant,

T is the absolute temperature in kelvins,

N_A is Avogadro's number.

e is the elementary charge,

or when the solute is mono-monovalent and symmetrical,

where

R is the gas constant,

F is the Faraday constant,

C₀ is the molar concentration of the electrolyte.

Alternatively,

where

λ_B is the Bjerrum length of the medium.

For water at room temperature, λ_B ≈ 0.7 nm.

References

• Goldston & Rutherford (1997). Introduction to Plasma Physics. Institute of Physics Publishing, Philadelphia. 

• Lyklema (1993). Fundamentals of Interface and Colloid Science. Academic Press, NY.