To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Double layer (plasma)
A double layer is a structure in a plasma and consists of two parallel layers with opposite electrical charge. The sheets of charge cause a strong electric field and a correspondingly sharp change in voltage (electrical potential) across the double layer. Ions and electrons which enter the double layer are accelerated, decelerated, or reflected by the electric field. In general, double layers (which may be curved rather than flat) separate regions of plasma with quite different characteristics. Double layers are found in a wide variety of plasmas, from discharge tubes to space plasmas to the Birkeland currents supplying the Earth's aurora, and are especially common in current-carrying plasmas. Compared to the sizes of the plasmas which contain them, double layers are very thin (typically ten Debye lengths), with widths ranging from a few millimeters for laboratory plasmas to thousands of kilometres for astrophysical plasmas. Other names for a double layer are: electrostatic double layer, electric double layer, plasma double layers, electrostatic shock (a type of double layer which is oriented at an oblique angle to the magnetic field in such a way that the perpendicular electric field is much larger than the parallel electric field),[6] space charge layer.[7] In laser physics, a double layer is sometimes called an ambipolar electric field.[8] Double layers are conceptually related to the concept of a 'sheath' (see Debye sheath). The adopted electrical symbol for a double layer, when represented in an electrical circuit is: ────DL──── If there is a net current present, then the DL is oriented so that the base of the L is in line with direction of current.[9] An overview of double layers in space, experiment and simulation is given in the introduction of ref.[10] Product highlight
Double layer classification
Double layers may be classified in the following ways:
Double layer formation
There are two different kinds of double layers, which are formed differently: Current carrying double layersCurrent carrying double layers may arise in plasmas carrying a current. Various instabilities can be responsible for the formation of these layers. One example is the Buneman instability which occurs when the streaming velocity of the electrons (basically the current density divided by the electron density) exceeds the electron thermal velocity of the plasma. Double layers (and other phase space structures) are often formed in the non-linear phase of the instability. One way of viewing the Buneman instability is to describe what happens when the current (in the form of a zero temperature electron beam) has to pass through a region of decreased ion density. In order to prevent charge from accumulating, the current in the system must be the same everywhere (in this 1D model). The electron density also has to be close to the ion density (quasineutrality), so there is also a dip in electron density. The electrons must therefore be accelerated into the density cavity, to maintain the same current density with a lower density of charge carriers. This implies that the density cavity is at a high electrical potential. As a consequence, the ions are accelerated out of the cavity, amplifying the density perturbation. Then there is the situation of a double-double layer, of which one side will most likely be convected away by the plasma, leaving a regular double layer. This is the process in which double layers are produced along planetary magnetic field lines in so-called Birkeland currents. Current-free double layersCurrent-free double layers occur at the boundary between plasma regions with different plasma properties. We explain how they form (neglecting the ions which are considered solely as a neutralizing background). Consider a plasma divided into two regions by a plane, which has a higher electron temperature on one side than on the other (the same analysis can also be done for different densities). This means that the electrons on one side of the interface have a greater thermal velocity. The electrons may stream freely in either direction, and the flux of electrons from the hot plasma to the cold plasma will be greater than the flux of the electrons from the cold plasma to the hot plasma, because the electrons from the hot side have a greater average speed. Because many more electrons enter the cold plasma than exit it, part of the cold region becomes negatively charged. The hot plasma, conversely, becomes positively charged. Therefore, an electric field builds up, which starts to accelerate electrons towards the hot region, reducing the net flux. In the end, the electric field builds up until the fluxes of electrons in either direction are equal, and further charge build up in the two plasmas is prevented. The potential drop is in fact exactly equal to the difference in thermal potential between the two plasma regions in this case, so such a double layer is a marginally strong double layer. Double layer formation mechanismsThe details of the formation mechanism depend on the environment of the plasma (eg. double layers in the laboratory, ionosphere, space plasmas, fusions plasma, etc). Proposed mechanisms for their formation have included:
Features and characteristics of double layers
History of double layersThe research of these objects is a relatively young phenomenon. Although it was already known in the 1920s that a plasma has a limited capacity for current maintenance, Irving Langmuir[49] characterized double layers in the laboratory and called these structures double-sheaths. It was not until the 1950s that a thorough study of double layers started in the laboratory (e.g. Schönhuber, 1958).[citation needed] At the moment many groups are working on this topic theoretically, experimentally and numerically. It was first proposed by Hannes Alfvén (the developer of magnetohydrodynamics) that the creation of the polar lights or Aurora Borealis is created by accelerated electrons in the magnetosphere of the Earth.[50] He supposed that the electrons were accelerated electrostatically by an electric field localized in a small volume bounded by two charged regions. This so-called double layer would accelerate electrons Earthwards. Many experiments with rockets and satellites have been performed to investigate the magnetosphere and acceleration regions. The first indication for the existence of electric field aligned along the magnetic field (or double layers) in the magnetosphere was by a rocket experiment by McIlwain (1960). Later, in 1977, Forrest Mozer reported that satellites had detected the signature of double layers (which he called electrostatic shocks) in the magnetosphere.[51] The most definite proof of these structures was obtained by the Viking satellite,[52] which measures the differential potential structures in the magnetosphere with probes mounted on 40 m long booms. These probes can measure the local particle density and the potential difference between two points 80m apart. Asymmetric potential structures with respect to 0 V were measured, which means that the structure has a net potential and can be regarded as a double layer. The particle densities measured in such structures can be as low as 33% of the background density. The structures usually have an extent of 100 m (a few tens of Debye lengths). The filling factor of the lower magnetosphere with such solitary structures is about 10%. If one out of 5 such structures has a net potential drop of 1 V then the total potential drop over a region of 5000 km would be more than the 1 kV which is needed for the electrons to create the aurora. Magnetospheric double layers typically have a strength A recent development in double layer experiments is the investigation of so-called stairstep double layers. It has been observed that a potential drop in a plasma column can be split up into different parts. Transitions from a single double layer into two, three or more-step double layers are strongly sensitive to the boundary conditions of the plasma (Hershkowitz, 1992).[citation needed] These experiments can give us information about the formation of the magnetospheric double layers and their possible role in creating the aurora. Some scientists have subsequently suggested a role of double layers in solar flares[55][56][57] Mathematical description of a double layer.In this section we will take a closer look at the mathematics behind double layers. We first describe a semi-quantitative criterion for the formation of a density dip. We then describe a particularly simple kind of double layer. We then explain how to use the distribution function and the Vlasov-Poisson equation to model more complex double layers. Formation of a density dip.First we will take a look at the generation of a double layer in a current carrying plasma. In 1968 Alfvén and Carlqvist showed that a density dip in a current carrying plasma can be favourable for the generation of a double layer. In this case we look at the plasma as a combination of two fluids, the moving electron fluid and the immobile ion fluid which acts as a neutralizing background. The electron fluid is treated as an essentially zero temperature beam and the ions are assumed to be collisional, and possess some finite temperature. The density dip in the plasma (of both electrons and ions) will cause an electric field to be generated in order to keep the current density at the same level, i.e. electrons are accelerated in the decreasing part into the dip and decelerated in the increasing part out of the dip. However, this electric field will also have an influence on the first as immobile assumed ions. These ions will be driven out of the density dip, increasing it, and thereby increasing the electric field. When all ions are gone, the electric field has reached its maximum value over the dip. Note that we then have a double-double layer (increasing and decreasing electric field), and one side needs to be transported away. We will use the quasi-static, non-relativistic description of this mechanism, which is governed by the continuity equation and the momentum equation:
Combining these two equations we get an expression for the electric field dependent on the electron density:
Current carrying double layers formed by single, zero temperature beams.We consider how a single zero-temperature beam of ions and a single zero-temperature beam of electrons, together with a trapped, zero velocity ion component, and a trapped, zero velocity electron component, may form a particular class of double layer. The trapped components are referred to as the 'ambient plasma' and will later be allowed to have finite temperature. We use Poisson's equation and the conservation of momentum and number density to analyse the structure of these double layers, in the 1D, time-independent limit. We are looking for double layer like solutions, where there is a well localised region with a potential gradient, outside of which the electric field is zero. The region can be divided into the interval inside the double layer, where there is only one ion component and one electron component, but there is a finite field, and the outside region, where the electric field is zero. For the moment, we need only consider the inside region and the densities and velocities associated with the beams inside the layer. The electron beam component is streaming with positive velocity ve(x) (to the right), and the ion beam is streaming with negative velocity vi(x) (to the left). Here, the conservation of particle energy means that
where φe = φ and φi = φDL − φ. Here n0 and vα,0 are respectively the electron (and ion) density and particle drift speed at the low (high) potential side of the double layer. Now we use Poisson’s equation to obtain the maximal current through the double layer, as a function of the potential drop, the fraction of current carried by the ions as compared to the electrons and a temperature limit for the ambient plasma. We chose φ(x = 0) = 0 and φ(x = d) = φDL, with d the thickness of the double layer.
Thus we can write Poisson’s equation in the region inside the double layer as:
Introducing an integration factor dφ / dx at both sides and integrating over x at the left hand side and over φ on the right hand side the first integration leads to the square of the electric field (dφ / dx)2. The assumption that there is no electric field outside the double layer then leads to the ‘’Langmuir condition’’ for non-relativistic double layers:
For this double layer (in a hydrogen plasma) the electron current dominates the ion current by a factor of
where C0 is expressed in terms of the elliptical integrals E and K:
If we now allow the ambient plasma to be at finite temperature we have to take into account reflected particles more carefully and examine how far they can penetrate into the repulsive electric field. We describe the ambient plasma by a Boltzmann distribution over the double layer:
The densities of the reflected particles are now added to Poisson’s equation. In order that the particles in the 'ambient plasma' be truly trapped we require that their temperature be lower than the double layer potential. This can be seen in terms of the restriction that the potential and the electric field have to vanish at the boundaries of the double layer. The precise condition is known as the ‘’Bohm criterion’’:
A double layer of this type cannot form if this criterion is not met. This is the same condition under which a double layer can be formed by an ion density dip (or equivalently, for instability to parallel wavemodes like the ion acoustic or Buneman instability) as discussed before. The Vlasov-Poisson equation.In general the plasma distributions near a double layer are necessarily strongly non-Maxwellian, and therefore inaccessible to fluid models. In order to analyse double layers in full generality, the plasma must be described using the particle distribution function The Vlasov-Poisson equations give the time-dependent interaction of a plasma (described using the particle distribution) with its self-consistent electric field. The Vlasov-Poisson equations are a combination of the Vlasov equations for each species α (also called the collisionless Boltzmann equation (CBE). We take the nonrelativistic zero-magnetic field limit);
and Poisson’s equation:
Here qα is the particle’s electric charge, mα is the particle’s mass, References
|
|||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Double_layer_(plasma)". A list of authors is available in Wikipedia. |





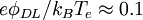 (where the electron temperature is assumed to lie in the range (
(where the electron temperature is assumed to lie in the range (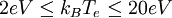 ) and are therefore weak.
In the laboratory double layers can be created in different devices. The are investigated in double plasma machines, triple plasma machines and Q-machines. The stationary potential structures which can be measured in these machines agree very well with what one would expect theoretically. An example of a laboratory double layer can be seen in the figure below, taken from Torvén and Linberg (1980), where we can see how well-defined and confined the potential drop of a double layer in a double plasma machine is.
One of the interesting things of the experiment by Torvén and Lindberg (1980)
) and are therefore weak.
In the laboratory double layers can be created in different devices. The are investigated in double plasma machines, triple plasma machines and Q-machines. The stationary potential structures which can be measured in these machines agree very well with what one would expect theoretically. An example of a laboratory double layer can be seen in the figure below, taken from Torvén and Linberg (1980), where we can see how well-defined and confined the potential drop of a double layer in a double plasma machine is.
One of the interesting things of the experiment by Torvén and Lindberg (1980)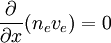
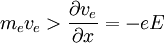
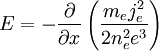 where
where 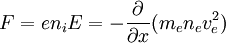 .
Only when the force of the electric field can overcome the force by the ion
.
Only when the force of the electric field can overcome the force by the ion 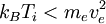 . This happens to be the Bohm criterion for the stability of a double layer (more below).
. This happens to be the Bohm criterion for the stability of a double layer (more below).
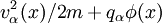 is a constant, and the conservation of particle number means that the current
is a constant, and the conservation of particle number means that the current 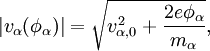
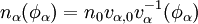
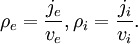
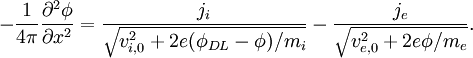
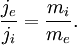
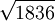 . (Note that for the same theory for ultra-relativistic double layers gives this fraction equal to 1). Further integration, as done by Raadu (1989), then leads to the Langmuir-Child relation:
. (Note that for the same theory for ultra-relativistic double layers gives this fraction equal to 1). Further integration, as done by Raadu (1989), then leads to the Langmuir-Child relation:
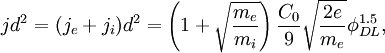
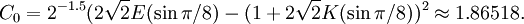
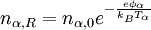
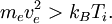
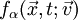 , which describes the number of particles of species
, which describes the number of particles of species 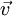 near the place
near the place 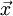 and time
and time 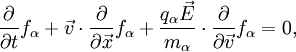
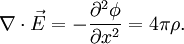
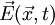 is the electric field,
is the electric field, 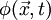 the electric potential and
the electric potential and 

