To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Debye sheathThe Debye sheath (also electrostatic sheath) is a layer in a plasma which has a greater density of positive ions, and hence an overall excess positive charge, that balances an opposite negative charge in the surface of a material in which it is in contact. The thickness of such a layer is several Debye lengths thick, a value whose size depends on various characteristics of plasma (eg. temperature, density, etc). A Debye sheath arises in a plasma because the electrons usually have a temperature on the order of or greater than that of the ions and are much lighter. Consequently they are faster than the ions by at least a factor of 40 ( The Debye sheath is the transition from a plasma to a solid surface. Similar physics is involved between two plasma regions that have different characteristics; the transition between these regions is known as a double layer, and features one positive, and one negative layer. Product highlight
DescriptionSheaths were first described by American physicist Irving Langmuir. In 1923 he wrote:
Langmuir and co-author Albert W. Hull further described a sheath formed in a thermionic valve:
Mathematical treatmentThe planar sheath equationThe quantitative physics of the Debye sheath is determined by four phenomena: Energy conservation of the ions: If we assume for simplicity cold ions of mass mi entering the sheath with a velocity u0, conservation of energy in the sheath potential requires
Ion continuity: In the steady state, the ions do not build up anywhere, so the flux is everywhere the same: n0u0 = ni(x)u(x). Boltzmann relation for the electrons: Since most of the electrons are reflected, their density is given by ne(x) = n0exp(eφ / kBTe). Poisson's equation: The curvature of the electrostatic potential is related to the net charge density as follows:
Combining these equations and writing them in terms of the dimensionless potential, position, and ion speed,
we arrive at the sheath equation:
The Bohm sheath criterionThe sheath equation can be integrated once by multiplying by χ':
At the sheath edge (ξ = 0), we can define the potential to be zero (χ = 0) and assume that the electric field is also zero (χ' = 0). With these boundary conditions, the integrations yield
This is easily rewritten as an integral in closed form, although one that can only be solved numerically. Nevertheless, an important piece of information can be derived analytically. Since the left-hand-side is a square, the right-hand-side must also be non-negative for every value of χ, in particular for small values. Looking at the Taylor expansion around χ = 0, we see that the first term that does not vanish is the quadratic one, so that we can require
or
or
This inequality is known as the Bohm sheath criterion after its discoverer, David Bohm. If the ions are entering the sheath too slowly, the sheath potential will "eat" its way into the plasma to accelerate them. Ultimately a so-called pre-sheath will develop with a potential drop on the order of (kBTe / 2e) and a scale determined by the physics of the ion source (often the same as the dimensions of the plasma). Normally the Bohm criterion will hold with equality, but there are some situations where the ions enter the sheath with supersonic speed. The Child-Langmuir LawAlthough the sheath equation must generally be integrated numerically, we can find an approximate solution analytically by neglecting the e − χ term. This amounts to neglecting the electron density in the sheath, or only analyzing that part of the sheath where there are no electrons. For a "floating" surface, i.e. one that draws no net current from the plasma, this is a useful if rough approximation. For a surface biased strongly negative so that it draws the ion saturation current, the approximation is very good. It is customary, although not strictly necessary, to further simplify the equation by assuming that
As before, we multiply by χ' and integrate to obtain
or
This is easily integrated over ξ to yield
where χw is the (normalized) potential at the wall (relative to the sheath edge), and d is the thickness of the sheath. Changing back to the variables u0 and φ and noting that the ion current into the wall is J = en0u0, we have
This equation is known as Child's Law, after Clement Dexter Child (1868-1933), who first published it in 1911, or as the Child-Langmuir Law, honoring as well Irving Langmuir, who discovered it independently and published in 1913. It was first used to give the space-charge-limited current in a vacuum diode with electrode spacing d. It can also be inverted to give the thickness of the Debye sheath as a function of the voltage drop by setting
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Debye_sheath". A list of authors is available in Wikipedia. |


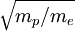 ). At the interface to a material surface, therefore, the electrons will fly out of the plasma, charging the surface negative relative to the bulk plasma. Due to
). At the interface to a material surface, therefore, the electrons will fly out of the plasma, charging the surface negative relative to the bulk plasma. Due to 


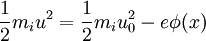 .
.
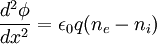 .
.
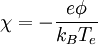
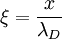
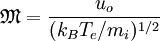
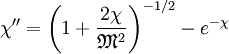 .
.
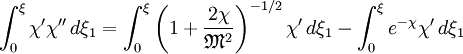
![\frac{1}{2}\chi'^2 = \mathfrak{M}^2 \left[ \left( 1 + \frac{2\chi}{\mathfrak{M}^2} \right)^{1/2} - 1 \right] + e^{-\chi} - 1](images/math/5/0/4/50409c5bc3c0b3cf3047d8070cb4427e.png)
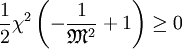 ,
,
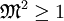 ,
,
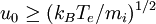 .
.
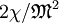 is much larger than unity. Then the sheath equation takes on the simple form
is much larger than unity. Then the sheath equation takes on the simple form
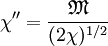 .
.
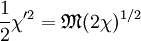 ,
,
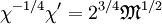 .
.
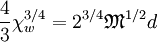 ,
,
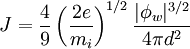 .
.
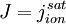 :
:
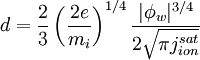 .
.


