To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Boltzmann relationIn a plasma, the Boltzmann relation connects the electron density ne to the plasma potential φpl as follows:
Product highlightThe reference for the potential is taken to be a position where the electron density is n0. It can be derived in a particle view by equating the density of states to the physical density and applying the Boltzmann factor. Alternatively, it can be derived from the fluid equation for the electrons by equating the force density due to the electron pressure gradient assuming isothermal electrons, In many problems of plasma physics, it is not useful to calculate the electric potential on the basis of the Poisson equation because the electron and ion densities are not known a priori, and if they were, because of quasineutrality the net charge density is the small difference of two large quantities, the electron and ion charge densities. If the ion density is known and the assumptions hold sufficiently well, the electric potential can be calculated simply from the Boltzmann relation. Discrepancies with the Boltzmann relation can occur, for example, when oscillations occur so fast that the electrons cannot find a new equilibrium (see e.g. plasma oscillations) or when the electrons are prevented from moving by a magnetic field (see e.g. lower hybrid oscillations). |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Boltzmann_relation". A list of authors is available in Wikipedia. |





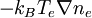 , to the force density due to the electric field on the electron charge density,
, to the force density due to the electric field on the electron charge density, 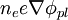 .
.


