To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Plasma oscillationIn plasma physics, plasma oscillations, also known as "Langmuir waves" (after Irving Langmuir) and "plasma waves," are periodic oscillations of charge density in conducting media such as plasmas or metals. The particle resulting from the quantization of these oscillations is the plasmon. Product highlight
ExplanationConsider a neutral plasma, consisting of a gas of positively charged ions and negatively charged electrons. If one displaces by a tiny amount all of the electrons with respect to the ions, the Coulomb force pulls back, acting as a restoring force. 'Cold' electronsIf the electrons are cold, it is possible to show that the charge density oscillates at the plasma frequency
where ne is the density of electrons, e is the electric charge, m is the mass of the electron, and ε0 is the permittivity of free space. Note that the above formula is derived under the approximation that the ion mass is infinite. This is generally a good approximation, as the electrons are so much lighter than ions. (One must modify this expression in the case of electron-positron plasmas, often encountered in astrophysics). Since the frequency is independent of the wavelength, these oscillations have an infinite phase velocity and zero group velocity. 'Warm' electronsIf warm electrons are considered with an electron thermal speed ve,th = ((kBTe)/(me))1/2 , the electron pressure acts as a restoring force as well as the electric field and the oscillations propagate with frequency and wavenumber related by
called the Bohm-Gross dispersion relation. If the spatial scale is large compared to the Debye length, the oscillations are only weakly modified by the pressure term, but at small scales the pressure term dominates and the waves become dispersionless with a speed of 31/3ve,th. For such waves, however, the electron thermal speed is comparable to the phase velocity, i.e., so the plasma waves can accelerate electrons that are moving with speed nearly equal to the phase velocity of the wave. This process often leads to a form of collisionless damping, called Landau damping. Consequently, the large-k portion in the dispersion relation is difficult to observe and seldom of consequence. In a bounded plasma, fringing electric fields can result in propagation of plasma oscillations, even when the electrons are cold. In a metal or semiconductor, the effect of the ions' periodic potential must be taken into account. This is usually done by using the electrons' effective mass in place of m. Langmuir wavesLangmuir waves are longitudinal plasma oscillations. In waves of the form Langmuir waves were discovered by American physicists Irving Langmuir and Lewi Tonks in the 1920s. They are parallel in form to Jeans instability waves, which are caused by gravitational instabilities in a static medium. In 2006, plasma physicists at the Universities of Texas and Michigan were able to photograph Langmuir waves, generated by a 30 TW laser pulse, for the first time.[1] See also
References
Categories: Waves in plasmas | Plasma physics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Plasma_oscillation". A list of authors is available in Wikipedia. |





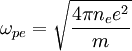 (cgs units)
(cgs units) 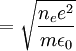 (
(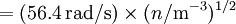 ,
,
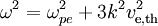 ,
,
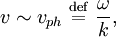
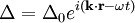 , Langmuir waves are governed by
, Langmuir waves are governed by 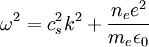 where
where 

