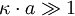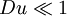Zeta potential

Zeta potential is an abbreviation for electrokinetic potential in colloidal systems. In the colloidal chemistry literature, it is usually denoted using the Greek letter zeta, hence ζ-potential. From theoretical viewpoint, zeta potential is electric potential in the interfacial double layer (DL) at the location of the slipping plane versus a point in the bulk fluid away from the interface. In other words, zeta potential is the potential difference between the dispersion medium and the stationary layer of fluid attached to the dispersed particle.

Zeta potential units are mV. The value of 25 mV can be taken as the boundary that separates low-charged surfaces from highly-charged surfaces.

The significance of zeta potential is that its value can be related to the stability of colloidal dispersions. Colloids with high zeta potential (negative or positive) are electrically stabilized. Colloids with low zeta potentials tend to coagulate or flocculate as outlined in the table^[1].

Zeta potential is widely used for quantification of the magnitude of the electrical charge at the double layer. However, zeta potential is not equal to the Stern potential or electric surface potential in the double layer. Such assumptions of equality should be applied with caution. Nevertheless, zeta potential is often the only available path for charaterization of double-layer properties. Zeta potential should not be confused with electrode potential or electrochemical potential (because electrochemical reactions are generally not involved in the development of zeta potential).

Additional recommended knowledge

Daily Sensitivity Test

What is the Sensitivity of my Balance?

Essential Laboratory Skills Guide

Methods for experimental determination of zeta potential

Zeta potential is not measurable directly but it can be calculated using theoretical models and an experimentally-determined electrophoretic mobility or dynamic electrophoretic mobility.

Electrokinetic phenomena and electroacoustic phenomena are the usual sources of data for calculation of zeta potential.

Electrokinetic phenomena

Main article: Electrokinetic phenomena

Electrophoresis is used for estimating zeta potential of particulates, whereas streaming potential/current is used for porous bodies and flat surfaces.

Electrophoresis

Main article: Electrophoresis

Electrophoretic velocity is proportional to electrophoretic mobility, which is the measurable parameter. There are several theories that link electrophoretic mobility with zeta potential. They are briefly described in the article on electrophoresis and in details in many books on Colloid and Interface Science^[2], ^[3], ^[4],^[5],^[6], ^[7]. There is an IUPAC Technical Report ^[8] prepared by a group of world experts on the electrokinetic phenomena.

From the instrumental viewpoint, there are two different experimental techniques:

• Microelectrophoresis. It has the advantage of yielding an image of the moving particles. On the other hand, it is complicated by electro-osmosis at the walls of the sample cell.

• Electrophoretic light scattering. It is based on dynamic light scattering. It allows measurement in an open cell, which eliminates the problem of electro-osmotic flow, but at the price of the lost ability to display images of moving particles.

Both these measuring techniques require extreme dilution of the sample. This dilution might affect properties of the sample and change zeta potential. There is only one justified way to perform this dilution - by using equilibrium supernate. Only in this case the interfacial equilibrium between the surface and the bulk liquid would be maintained and zeta potential would be the same for all volume fractions of particles in the suspension.

Streaming potential/current

Electroacoustic phenomena

There are two electroacoustic effects that are widely used for characterizing zeta potential : Colloid Vibration Current and Electric Sonic Amplitude, see reference^[7]. There are commercially available instruments that exploit these effects for measuring dynamic electrophoretic mobility, which depends on zeta potential.

Electroacoustic techniques have the advantage of being able to perform measurements in intact samples, without dilution. Published and well-verfied theories allow such measurements at volume fractions up to 50%, see reference^[7].

On the other hand, electroacoustic methods yield only a single average value for zeta potential, whereas the two other methods mentioned above provide information on the distribution of zeta potential.

Theory for Zeta potential calculation

The most known and widely-used theory for calculating zeta potential from experimental data is that developed by Smoluchowski in 1903 ^[9]. This theory was originally developed for electrophoresis; however, an extension to electroacoustics is now also available ^[7]. Smoluchowski's theory is powerful because it is valid for dispersed particles of any shape and any concentration. However, it has its limitations:

• Detailed theoretical analysis proved that Smoluchowski theory is valid only for a sufficiently thin DL, when the Debye length, 1/κ, is much smaller than the particle radius a:

The model of the "thin double layer" offers tremendous simplifications not only for electrophoresis theory but for many other electrokinetic and electroacoustic theories. This model is valid for most aqueous systems because the Debye length is typically only a few nanometers in water. The model breaks only for nano-colloids in a solution with ionic strength approaching that of pure water.

• Smoluchowski's theory neglects the contribution of surface conductivity. This is expressed in modern theories as the condition of a small Dukhin number:

The development of electrophoretic and electroacoustic theories with a wider range of validity was a purpose of many studies during 20th century. There are several analytical theories that incorporate surface conductivity and eliminate the restriction of the small Dukhin number for both the electrokinetic and electroacoustic applications.

Early pioneering work in that direction dates back to Overbeek ^[10] and Booth ^[11].

Modern, rigorous electrokinetic theories that are valid for any zeta potential and often any κa, stem mostly from the Ukrainian (Dukhin, Shilov and others) and Australian (O'Brien, White, Hunter and others) schools. Historically, the first one was Dukhin-Semenikhin theory ^[12]. A similar theory was created 10 years later by O'Brien and Hunter ^[13]. Assuming a thin double layer, these theories would yield results that are very close to the numerical solution provided by O'Brien and White ^[14].

There are also general electroacoustic theories that are valid for any values of Debye length and Dukhin number^[7][3]. Modern instruments for determining zeta potential are expected to have an option for selecting between the possible algorithms (including those based on the most modern theories).

References