Car-Parrinello method

The Car-Parrinello method in computational chemistry is a type of ab initio (first principles) molecular dynamics, usually employing periodic boundary conditions, planewave basis sets, and DFT.

In contrast to Born-Oppenheimer molecular dynamics wherein the nuclear (ions) degree of freedom are propagated using ionic forces which are calculated at each iteration by approximately solving the electronic problem with conventional matrix diagonalization methods, the Car-Parrinello method explicitly introduces the electronic degrees of freedom as (fictitious) dynamical variables, writing an extended Lagrangian for the system which leads to a system of coupled equations of motion for both ions and electrons. In this way an explicit electronic minimization at each iteration is not needed: after an initial standard electronic minimization, the fictitious dynamics of the electrons keep them on the electronic ground state corresponding to each new ionic configuration visited along the dynamics, thus yielding accurate ionic forces. In order to maintain this adiabaticity condition, it is necessary that the fictitious mass of the electrons is chosen small enough to avoid a significant energy transfer from the ionic to the electronic degrees of freedom. This small fictitious mass in turn requires that the equations of motion are integrated using a smaller time step than the ones (1-10 fs) commonly used in Born-Oppenheimer molecular dynamics.

Additional recommended knowledge

Essential Laboratory Skills Guide

How to quickly check pipettes?

Weighing the right way

Fictitious Dynamics

Lagrangian

Where is the Kohn-Sham energy density functional, which outputs energy values when given Kohn-Sham wavefunctions and nuclear positions.

Orthogonality Constraint

where δ_ij is the Kronecker Delta function.

Equations of Motion

You get the Equations of Motion by taking the stationary point of the Lagrangian with respect to ψ_i and R_I, with the orthogonality constraint.

Born-Oppenheimer Limit

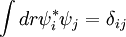
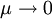In the formal limit where , the Equations of Motion approach Born-Oppenheimer Molecular Dynamics. However numerical implementation limit can lead to inefficient rapid oscillatory trajectories; given the integration framework and according to the problem, μ has to be chosen judiciously.

References

• R. Car and M. Parrinello, Phys. Rev. Lett. 55, 2471 (1985).
• Dominik Marx and Jurg Hutter (2000) Ab initio molecular dynamics: Theory and Implementation, Modern Methods and Algorithms of Quantum Chemistry J. Grotendorst (Ed.), Jonh von Neumann Institute for Computing, Julich, NIC Series, Vol. 1, ISBN 3-00-005618-1, pp. 301-449.

See also

Car-Parrinello Molecular Dynamics, a software package implementing the method.