Full configuration interaction

Full configuration interaction (or full CI) is a linear variational approach which provides numerically exact solutions (within the given one-particle basis set) to the electronic Schrödinger equation.

Additional recommended knowledge

Daily Visual Balance Check

Weighing the right way

Guide to balance cleaning: 8 simple steps

Explanation

It is a special case of the configuration interaction method in which all Slater determinants (or configuration state functions, CSFs) of the proper symmetry are included in the variational procedure (i.e. all Slater determinants obtained by exciting all possible electrons to all possible virtual orbitals, orbitals which are unoccupied in the electronic ground state configuration). This method is equivalent to computing the eigenvalues of the electronic molecular Hamiltonian within the basis set of the above mentioned configuration state functions.

In a minimal basis set a full CI computation is very easy. But in larger basis sets this is usually just a limiting case which is not often attained. The Davidson correction is a simple correction which allows one to estimate the value of the full-CI energy from a limited configuration interaction expansion result.

Because the number of determinants required in the full-CI expansion grows factorially with the number of electrons and orbitals, full CI is only possible for atoms or very small molecules with about a dozen or fewer electrons. Full CI problems including several million up to a few billion determinants are possible using current algorithms. Because full CI results are exact within the space spanned by the orbital basis set, they are invaluable in benchmarking approximate quantum chemical methods. This is particularly important in cases such as bond-breaking reactions, diradicals, and first-row transition metals, where electronic near-degeneracies can invalidate the approximations inherent in many standard methods such as Hartree-Fock theory, multireference configuration interaction, finite-order Møller-Plesset perturbation theory, and coupled cluster theory.

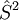Although fewer N-electron functions are required if one employs a basis of spin-adapted functions ( eigenfunctions), the most efficient full CI programs employ a Slater determinant basis because this allows for the very rapid evaluation of coupling coefficients using string-based techniques advanced by Nicholas C. Handy in 1980. In the 1980s and 1990s, full CI programs were adapted to provide arbitrary-order Møller-Plesset perturbation theory wave functions, and in the 2000s they have been adapted to provide coupled cluster wave functions to arbitrary orders, greatly simplifying the task of programming these complex methods.