To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Term symbolIn quantum mechanics, the term symbol is an abbreviated description of the angular momentum quantum numbers in a multi-electron atom. It is related with the energy level of a given electron configuration. LS coupling is assumed. The ground state term symbol is predicted by Hund's rules. The term symbol has the form
When used to describe electron states in an atom, the term symbol usually follows the electron configuration, e.g., in the case of carbon, the ground state is 1s22s22p2 3P0. The term symbol is also used to describe compound systems such as mesons or atomic nuclei, or even molecules (see molecular term symbol). In that last case, Greek letters are used to designate the (molecular) orbital angular momenta. For a given electron configuration
As an example, for S = 1, L = 2, there are (2×1+1)(2×2+1) = 15 different microstates corresponding to the 3D term, of which (2×3+1) = 7 belong to the 3D3 (J=3) level. The sum of (2J+1) for all levels in the same term equals (2S+1)(2L+1). In this case, J can be 1, 2, or 3, so 3 + 5 + 7 = 15. Product highlight
Term symbol parityThe parity of a term symbol is calculated as
where li is the orbital quantum number for each electron. In fact, only electrons in odd orbitals contribute to the total parity: an odd number of electrons in odd orbitals (those with an odd l such as in p, f,...) will make an odd term symbol, while an even number of electrons in odd orbitals will make an even term symbol, irrespective of the number of electrons in even orbitals. When it is odd, the parity of the term symbol is indicated by a superscript letter "o", otherwise it is omitted:
Alternatively, parity may be indicated with a subscript letter "g" or "u", standing for gerade (even in German) or ungerade (odd):
Ground state term symbolIt is relatively easy to calculate the term symbol for the ground state of an atom. It corresponds with a state with maximal S and L.
As an example, in the case of fluorine, the electronic configuration is: 1s22s22p5. 1. Discard the full subshells and keep the 2p5 part. So we have five electrons to place in subshell p (l = 1). 2. There are three orbitals (ml = 1, 0, −1) that can hold up to 2(2l+1) = 6 electrons. The first three electrons can take ms = 1/2 (↑) but the Pauli exclusion principle forces the next two to have ms = −1/2 (↓) because they go to already occupied orbitals.
3. S = 1/2 + 1/2 + 1/2 − 1/2 − 1/2 = 1/2; and L = 1 + 0 − 1 + 1 + 0 = 1, which is "P" in spectroscopic notation; 4. As fluorine 2p subshell is more than half filled, J = L + S = 3/2. Its ground state term symbol is then Term symbols for an electron configurationTo calculate all possible term symbols for a given electron configuration the process is a bit longer.
Alternative methodAn alternative, much quicker method of arriving at the same result can be obtained from group theory. The configuration 2p2 has the symmetry of the following direct product in the full rotation group:
which, using the familiar labels Γ(0) = S, Γ(1) = P & Γ(2) = D, can be written as
The square brackets enclose the anti-symmetric square. Hence the 2p2 configuration has components with the following symmetries:
The Pauli principle and the requirement for electrons to be described by anti-symmetric wavefunctions imply that only the following combinations of spatial and spin symmetry are allowed:
Then one can move to step five in the procedure above, applying Hund's rules. The group theory method can be carried out for other such configurations, like 3d2, using the general formula
The symmetric square will give rise to singlets (such as 1S, 1D & 1G), while the anti-symmetric square gives rise to triplets (such as 3P & 3F). More generally, one can use
where, since the product is not a square, it is not split into symmetric and anti-symmetric parts. Where two electrons come from inequivalent orbitals, both a singlet and a triplet are allowed in each case. See also |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Term_symbol". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


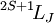



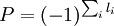 ,
,
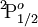 has odd parity, but
has odd parity, but 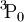 has even parity.
has even parity.
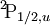 for odd parity and
for odd parity and 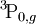 for even.
for even.
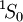 .
.
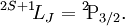
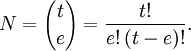
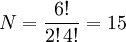
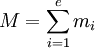 where mi is either ml or ms for the i-th electron, and M represents the resulting ML or MS respectively:
where mi is either ml or ms for the i-th electron, and M represents the resulting ML or MS respectively:


