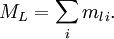To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Molecular term symbolIn molecular physics, the molecular term symbol is a shorthand expression of the group representation and angular momenta that characterize the state of a molecule, i.e. its electronic quantum state which is an eigenstate of the electronic molecular Hamiltonian. It is the equivalent of the term symbol for the molecule case. However, the following presentation is restricted to the case of homonuclear diatomic molecules, or symmetric molecules with an inversion centre. For heteronuclear diatomic molecules, the u/g symbol does not correspond to any exact symmetry of the electronic molecular Hamiltonian. In the case of less symmetric molecule the molecular term symbol contains the symbol of the group representation to which the molecular electronic state belongs. It has the general form: where
Product highlight
Λ quantum numberFor atoms, we use S, L, J and MJ to characterize a given state. In linear molecules, however, the lack of spherical symmetry destroys the relationship The cylindrical symmetry of a linear molecule ensures that positive and negative values of a given ml for an electron in a molecular orbital will be degenerate in the absence of spin-orbit coupling. Different molecular orbitals are classified with a new quantum number, λ, defined as
Following the spectroscopic notation pattern, molecular orbitals are designated by a smallcase Greek letter: for λ = 0, 1, 2, 3,... orbitals are called σ, π, δ, φ... respectively. Now, the total z-projection of L can be defined as As states with positive and negative values of ML are degenerate, we define
and a capital Greek letter is used to refer to each value: Λ = 0, 1, 2, 3... are coded as Σ, Π, Δ, Φ... respectively. The molecular term symbol is then defined as
and the number of electron degenerate states (under the absence of spin-orbit coupling) corresponding to this term symbol is given by:
Ω and spin-orbit couplingSpin-orbit coupling lifts the degeneracy of the electronic states. This is because the z-component of spin interacts with the z-component of the orbital angular momentum, generating a total electronic angular momentum along the molecule axis Jz. This is characterized by the MJ quantum number, where
Again, positive and negative values of MJ are degenerate, so the pairs (ML, MS) and (−ML, −MS) are degenerate: {(1, 1/2), (−1, −1/2)}, and {(1, −1/2), (−1, 1/2)} represent two different degenerate states. These pairs are grouped together with the quantum number Ω, which is defined as the sum of the pair of values (ML, MS) for which ML is positive. Sometimes the equation
is used (often Σ is used instead of MS). Note that although this gives correct values for Ω it could be misleading, as obtained values do not correspond to states indicated by a given pair of values (ML,MS). For example, a state with (−1, −1/2) would give an Ω value of Ω = |−1| + (−1/2) = −1/2, which is wrong. Choosing the pair of values with ML positive will give a Ω = 3/2 for that state. With this, a level is given by
Note that Ω can have negative values. For a 4Π term there are four degenerate (ML, MS) pairs: {(1, 3/2), (−1, −3/2)}, {(1, 1/2), (−1, −1/2)}, {(1, −1/2), (−1, 1/2)}, {(1, −3/2), (−1, 3/2)}. These correspond to Ω values of 5/2, 3/2, 1/2 and −1/2, respectively. Approximating the spin-orbit Hamiltonian to first order perturbation theory, the energy level is given by
where A is the spin-orbit constant. For 4Π the Ω values 5/2, 3/2, 1/2 and −1/2 correspond to energies of 3A/2, A/2, −A/2 and −3A/2. Despite of having the same magnitude, levels of Ω = ±1/2 have different energies associated, so they are not degenerate. With that convention, states with different energies are given different Ω values. For states with positive values of A (which are said to be regular), increasing values of Ω correspond to increasing values of energies; on the other hand, with A negative (said to be inverted) the energy order is reversed. Including higher order effects can lead to a spin-orbital levels or energy that do not even follow the increasing value of Ω. When Λ = 0 there is no spin-orbit splitting to first order in perturbation theory, as the associated energy is zero. So for a given S, all of its MS values are degenerate. This degeneracy is lifted when spin-orbit interaction is treated to higher order in perturbation theory, but still states with same |MS| are degenerate in a non-rotating molecule. We can speak of a 5Σ2 substate, a 5Σ1 substate or a 5Σ0 substate. Except for the case Ω = 0, these substates have a degeneracy of 2. Reflexion through a plane containing the internuclear axisThere are infinite planes containing the internuclear axis, so there are infinite possible reflexions. For any of these planes, molecular terms with Λ > 0 always have a state which is symmetric with respect to this reflection and one state that is antisymmetric. Rather than labelling those situations as, e.g., 2Π±, the ± is omitted. For the Σ states, however, this two-fold degeneracy disappears, and all Σ states are either symmetric under any plane containing the internuclear axis, or antisymmetric. These two situations are labeled as Σ+ or Σ−. Reflexion through an inversion center: u and g symmetryTaking the molecule center of mass as origin of coordinates, consider the change of all electrons' position from (xi, yi, zi) to (−xi, −yi, −zi). If the resulting wave function is unchanged, it is said to be gerade (German for even); if the wave function changes sign then it is said to be ungerade (odd). For a molecule with a center of inversion, all orbitals will be symmetric or antisymmetric. The resulting wavefunction for the whole multielectron system will be gerade if an even number of electrons is in ungerade orbitals, and ungerade if there is an odd number of electrons in ungerade orbitals, independently of the number of electrons in gerade orbitals. Categories: Molecular physics | Quantum chemistry | Atomic physics | Spectroscopy |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Molecular_term_symbol". A list of authors is available in Wikipedia. |


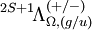



![[\hat\mathbf L^2, \hat H]=0](images/math/c/9/a/c9a5824042c1e8de5550a501fa86d581.png) , so L ceases to be a good quantum number. A new set of operators have to be used instead:
, so L ceases to be a good quantum number. A new set of operators have to be used instead: 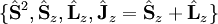 , where the z-axis is defined along the internuclear axis of the molecule. Since these operators commute with each other and with the Hamiltonian on the limit of negligible spin-orbit coupling, their eigenvalues may be used to describe a molecule state through the quantum numbers S, MS, ML and MJ.
, where the z-axis is defined along the internuclear axis of the molecule. Since these operators commute with each other and with the Hamiltonian on the limit of negligible spin-orbit coupling, their eigenvalues may be used to describe a molecule state through the quantum numbers S, MS, ML and MJ.