To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
List of Hund's rulesIn atomic physics, Hund's rules, (occasionally called the "bus seat rule") refer to a simple set of rules used to determine which is the term symbol that corresponds to the ground state of a multi-electron atom. They are named in honour of Friedrich Hund who contributed Hund's Rule, rule two as listed here. The four rules are:
The rules deal in a simple way how the usual energy interactions dictate the ground state term. The rules assume that the repulsion between the outer electrons is very much greater than the spin-orbit interaction which is in turn stronger than any other remaining interactions. This is referred to as the LS coupling regime. Product highlight
Rule #1It can be shown that for full orbitals and suborbitals both the residual electrostatic term (repulsion between protons) and the spin-orbit interaction cannot shift all the energy levels together. Thus when determining the ordering of energy levels in general only the inner valence electrons need to be considered. Rule #2Due to the Pauli exclusion principle, two electrons cannot share the same set of quantum numbers within the same system. Therefore, there is room for only two electrons in each spatial orbital. One of these electrons must have (for some chosen direction z), It is often stated that this is the highest energy atomic state because it forces the paired electrons to reside in different spatial orbitals, and this results in a larger average distance between the two electrons, reducing electron-electron repulsion energy. But, in fact, careful calculations have shown that this explanation can be wrong, at least for light systems. Rule #3This rule deals again with reducing the repulsion between electrons. It can be understood from the classical picture that if all electrons are orbiting in the same direction (higher orbital angular momentum) they meet less often than if some of them orbit in opposite directions. In that last case the repulsive force increases, which separates electrons. This adds potential energy to them, so their energy level is higher. Rule #4This rule considers the energy shifts due to split-orbit coupling. In the case where the spin-orbit coupling is weak compared to the residual electrostatic, where The value of Example
As an example, consider the ground state of silicon. The electronic configuration of Si is NotesHund's rules are often used to order the inner levels. This is a common misapplication of the rules and is generally incorrect. See alsoFor the notation of orbital angular momentum L see: Spectroscopic notation References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "List_of_Hund's_rules". A list of authors is available in Wikipedia. |


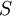 ) has the lowest energy level.
) has the lowest energy level.
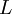 has the lowest energy in an orbital.
has the lowest energy in an orbital.
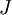 lies lowest in energy. Otherwise, if the outermost shell is more than half-filled, the term with highest value of
lies lowest in energy. Otherwise, if the outermost shell is more than half-filled, the term with highest value of 


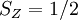 , and the other must have
, and the other must have 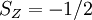 . Hund's second rule states that the lowest energy atomic state is the one which maximizes the sum of the
. Hund's second rule states that the lowest energy atomic state is the one which maximizes the sum of the 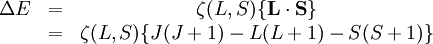
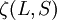 changes from minus to plus for shells less than half full. The first term gives the dependence of the ground state on the magnitude of
changes from minus to plus for shells less than half full. The first term gives the dependence of the ground state on the magnitude of 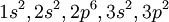 . Applying the first rule, only the outer
. Applying the first rule, only the outer 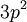 electrons need be considered. The possible multiplets are
electrons need be considered. The possible multiplets are 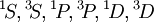 ; of those,
; of those, 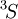 and
and 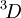 are not allowed because of the exclusion principle. The second rule now states that the triplet state
are not allowed because of the exclusion principle. The second rule now states that the triplet state 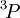 with
with 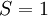 has the lowest energy. There is no choice of triplets
has the lowest energy. There is no choice of triplets 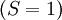 states, so the first rule is not required. [If the
states, so the first rule is not required. [If the 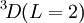 state were allowed, then the third rule would come into force and state that it was more favourable than the
state were allowed, then the third rule would come into force and state that it was more favourable than the 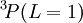 state.] The triplet
state.] The triplet 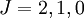 . With only two of six possible electrons in the shell, it is less than half-full and thus
. With only two of six possible electrons in the shell, it is less than half-full and thus 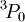 is the ground state.
is the ground state.


