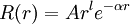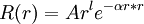Gaussian orbital

In molecular physics, Gaussian orbitals (also known as Gaussian type orbitals, GTOs or Gaussians) are functions used as atomic orbitals in the LCAO method for the computation of electron orbitals in molecules.

Additional recommended knowledge

Guide to balance cleaning: 8 simple steps

Safe Weighing Range Ensures Accurate Results

What is the Sensitivity of my Balance?

Rationale

The principal reason for the use of Gaussian basis functions in molecular quantum chemical calculations is the 'Gaussian Product Theorem', which guarantees that the product of two GTOs centered on two different atoms is a finite sum of Gaussians centered on a point along the axis connecting them. In this manner, four-center integrals can be reduced to finite sums of two-center integrals, and in a next step to finite sums of one-center integrals. The speedup by 4--5 orders of magnitude compared to Slater orbitals more than outweighs the extra cost entailed by the larger number of basis functions generally required in a Gaussian calculation.

For reasons of convenience, many Gaussian integral evaluation programs work in a basis of Cartesian Gaussians even when spherical Gaussians are requested: the 'contaminants' are deleted a posteriori.

Correct form of atomic orbitals:

GTO:

Molecular integrals

Molecular integrals over cartesian gaussian functions were first proposed by Boys^[1] in 1950. Since then much work has been done to speed up the evaluation of these integrals which are the slowest part of many quantum chemical calculations. McMurchie and Davidson (1978) introduced Hermite Gaussian functions to take advantage of differential relations. Pople and Hehre (1978) developed a local coordinate method. Obara and Saika introduced efficient recursion relations in 1985, which was followed by the development of other important recurrence relations. Gill and Pople (1990) introduced a 'prism' algorithm which allowed efficient use of 20 different calculation paths.

References