To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Spin-orbitalIn quantum mechanics, a spin-orbital is a one-particle wavefunction taking both the position and spin angular momentum of a particle as its parameters. Product highlightThe spinorbital of a single electron, for example, is a complex-valued function of four real variables: the three scalars used to define its position, and a fourth scalar, ms, which can be either +1/2 or −1/2:
We can also write it more compactly as a function of a position vector
For a general particle with spin s, ms can take values between −s to s in integer steps. The electron has s=1/2. A spinorbital is usually normalized, such that the probability of finding the particle anywhere in space with any spin is equal to 1: From a normalized spinorbital, one can calculate the probability that the particle is in an arbitrary volume of space V and has an arbitrary spin ms: |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Spin-orbital". A list of authors is available in Wikipedia. |





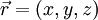 and the quantum number ms:
and the quantum number ms:
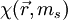 .
.