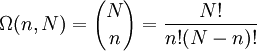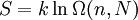Multiplicity function for N noninteracting spins

The multiplicity function for a two state paramagnet, Ω(n,N), is the number of spin states such that n of the N spins point in the z-direction. This function is given by the combinatoric function C(N,n). That is:

Additional recommended knowledge

How to ensure accurate weighing results every day?

Daily Visual Balance Check

Essential Laboratory Skills Guide

$\Omega (n,N) = {N \choose n} = {{N!} \over {n!(N - n)!}}$

It is primarily used in introductory statistical mechanics and thermodynamics textbooks to explain the microscopic definition of entropy to students. If the spins are non-interacting, then the multiplicity function counts the number of states which have the same energy in an external field magnetic field. By definition, the entropy S is then given by the natural logarithm of this number:

$S = k\ln \Omega (n,N) \,$ ^[1] Where k is the Boltzmann constant