Abeles matrix formalism

This article or section is in need of attention from an expert on the subject.

WikiProject Physics may be able to help recruit one.
If a more appropriate WikiProject or portal exists, please adjust this template accordingly.

The Abeles matrix method is a computationally fast and easy way to calculate the specular reflectivity from a stratified interface, as a function of the perpendicular momentum transfer, Q_z.

Additional recommended knowledge

Recognize and detect the effects of electrostatic charges on your balance

What is the Sensitivity of my Balance?

Essential Laboratory Skills Guide

Application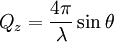

$Q_z=\frac{4\pi}{\lambda}\sin\theta$

Where θ is the angle of incidence/reflection of the incident radiation and λ is the wavelength of the radiation. The measured reflectivity depends on the variation in the scattering length density (SLD) profile, (ρ(z)) perpendicular to the interface. Although the scattering length density profile is normally a continuously varying function, the interfacial structure can often be well ap- proximated by a slab model in which layers of thickness (d_n), scattering length density (ρ_n) and roughness (σ_n,n+1)are sandwiched between the super- and sub-phases. One then uses a refinement procedure to minimise the differences between the theoretical and measured reflectivity curves, by changing the parameters that describe each layer.

In this description the interface is split into n layers. Since the incident neutron beam is refracted by each of the layers the wavevector, k, in layer n, is given by: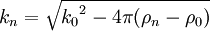

$k_n=\sqrt{{k_0}^2-4\pi({\rho}_n-{\rho}_0)}$

The Fresnel reflection coefficient between layer n and n+1 is then given by: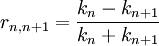

$r_{n,n+1} = \frac{k_{n}-k_{n+1}}{k_{n}+k_{n+1}}$

Since the interface between each layer is unlikely to be perfectly smooth the roughness/diffuseness of each interface modifies the Fresnel coefficient and is accounted for by an error function, as described by Nevot and Croce.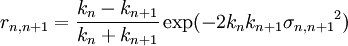

$r_{n,n+1} = \frac{k_{n}-k_{n+1}}{k_{n}+k_{n+1}}\exp(-2k_{n}k_{n+1}{\sigma_{n,n+1}}^2)$

A phase factor, β is introduced, which accounts for the thickness of each layer.

β n = k n d n

A characteristic matrix,c_n is then calculated for each layer.

$c_{n}=\left[\begin{array}{cc} \exp\left(\beta_{n}\right) & r_{n}\exp\left(\beta_{n}\right)\\ r_{n}\exp\left(-\beta_{n}\right) & \exp\left(-\beta_{n}\right)\end{array}\right]$

The resultant matrix is defined as the product of these characteristic matrices, from which the reflectivity is calculated.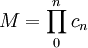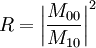

$M=\prod_{0}^{n}c_{n}$

$R=\left|\frac{M_{00}}{M_{10}}\right|^{2}$

References

OS Heavens. Optical Properties of Thin Films. Butterworth, London, 1955

Abeles matrix formalism

Additional recommended knowledge

Recognize and detect the effects of electrostatic charges on your balance

What is the Sensitivity of my Balance?

Essential Laboratory Skills Guide

Application

References

See also

About chemeurope.com

About LUMITOS

Advertise with LUMITOS