To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Momentum transferIn particle physics, wave mechanics and optics, momentum transfer is the amount of momentum that one particle gives to another particle. Product highlight
Free particlesIn the simplest example of scattering of two particles with momenta p1,p2 going into two particles with momenta p3,p4, the momentum transfer is given by
where the last identity expresses momentum conservation. Momentum transfer is an important quantity because Wave mechanics and opticsA wave has a momentum DiffractionThe momentum transfer plays an important role in the evaluation of neutron, X-ray and electron diffraction for the investigation of condensed matter. Bragg diffraction occurs on the atomic crystal lattice, conserves the wave energy and thus is called elastic scattering, where the wave numbers final and incident particles, kF and ki, respectively, are equal and just the direction changes by a reciprocal lattice vector G = Q = kf − ki with the relation to the lattice spacing G = 2π / d. The presentation in Q-space is generic and does not depend on the type of radiation and wavelength used but only on the sample system, which allows to compare results obtained from the many different methods. Some established communities such as powder diffraction employ the diffraction angle 2θ as the independent variable, which worked fine in the early years when only a few characteristic wavelengths such as Cu-Kalpha were available. The relationship to Q-space is
and basically states for simple minds, larger 2θ corresponds to larger Q. See also
Categories: Neutron related techniques | Diffraction |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Momentum_transfer". A list of authors is available in Wikipedia. |





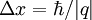 is a better measure for the typical distance resolution of the reaction than the momenta themselves.
is a better measure for the typical distance resolution of the reaction than the momenta themselves.
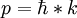 and is a vectorial quantity. The difference of the momentum of the scattered wave to the incident wave is called momentum transfer. The wave number k is the absolute of the wave vector
and is a vectorial quantity. The difference of the momentum of the scattered wave to the incident wave is called momentum transfer. The wave number k is the absolute of the wave vector 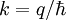 and is related to the wavelength
and is related to the wavelength