To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Active laser medium
Within a laser, the active laser medium or gain medium is the material that exhibits optical gain. This gain is generally generated by stimulated emission on electronic or molecular transitions to a lower energy state, starting from a higher energy state to which it had been previously stimulated by means of a pump source. Examples of active laser media include:
Pumping of gain media (i.e., the supply of energy) can be achieved with electrical currents (e.g. in semiconductors, or in gases via high-voltage discharges) or with light, which may be generated with discharge lamps or with other lasers (often semiconductor lasers, see DPSS laser). More exotic gain media can be pumped by chemical reactions (see chemical laser), nuclear fission (see nuclear pumped laser), or with high-energy electron beams.[1]. Product highlight
Example of a model of gain mediumThere is no universal model, which would be valid for all types of lasers [2]: . The simplest model includes two systems of sublevels, upper (2) and lower (1). Within each level the fast transitions
lead to the Boltzman distribution of excitations among sublevels (fig.1). The upper level is assumed to be metastable.
In this approximation, neither gain, nor refractive index depend on the particular way of excitation. For good performance of the
gain medium, the separation between sublevels should be larger than working temperature, then, at the pump frequency
The model below seems to work well for most of optically-pumped solid-state lasers. For other types of lasers, (for example, chemical lasers or gas-dynamical lasers) more complicated analysis is required. Cross-sectionsThe simple medium can be characterized with effective cross-sections of
absorption
and
emission
at frequencies
The relative concentrations can be defined as
The rate of transitions of an active center from ground state to the excited state can be expressed with
Then, the kinetic equation for relative populations can be written as follows:
However, these equations keep
The absorption
Steady-state solutionIn many cases, the gain medium works in continuous-wave or quasi-contiunuous regime, then the time derrivatives of populations are negligible. The steady-state solution can be written
The dynamic saturation intensities can be defined with
The gain at strong pump
where
Gain never exceeds value At given intensities
where
IdentitiesThe following identities [3] take place:
The state of gain medium can be characterized with a single parameter. Such a parameter can be population of the upper level, gain or absorption; other parameters can be expressed with the relations above. Efficiency of the gain mediumThe efficiency of a gain medium can be defined as
Without loss of laser cavity, this efficiency would be optical to optical efficiency of the laser. Within the same model, the efficiency can be expressed as follows:
For the efficient operation, both intensities, pump and signal should exceed their saturation intensities;
The estimates above are valid for the medium uniformly filled with pump and signal light. The spatial hole burning may slightly reduce the efficiency, because some region are pumped well, but the pump is not efficiently withdrawn by the signal in the nodes of the interference of counter-propagating waves. See alsoReferences and notes
Categories: Lasers | Laser gain media |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Active_laser_medium". A list of authors is available in Wikipedia. |





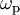 ,
the absorption dominates, and the emission (preferably, stimulated emission is dominant at the laser frequency
,
the absorption dominates, and the emission (preferably, stimulated emission is dominant at the laser frequency
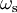 . In the case of amplification of optical signals, the lasing frequency is called
signal frequency. However, the same term is used even in the laser oscillators, when the amplified radiation is used
to transfer energy rather than some information.
. In the case of amplification of optical signals, the lasing frequency is called
signal frequency. However, the same term is used even in the laser oscillators, when the amplified radiation is used
to transfer energy rather than some information.
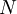 be concentration of active centers. This is typical state in the solid-state lasers.
Let
be concentration of active centers. This is typical state in the solid-state lasers.
Let 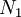 be concentration of active centers in the ground state and
Let
be concentration of active centers in the ground state and
Let 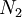 be concentration of excited centers;
Let
be concentration of excited centers;
Let 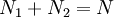 .
.
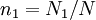 and
and
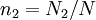 .
.
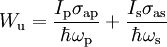 and
The rate of transitions back to the ground state can be expressed with
and
The rate of transitions back to the ground state can be expressed with
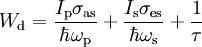 ,
where
,
where
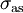 and
and
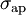 are effective cross-sections of the absorption at the frequencies of the
pump and the signal, and
are effective cross-sections of the absorption at the frequencies of the
pump and the signal, and
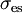 and
and
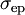 are the same for stimulated emission;
are the same for stimulated emission;
 is rate of the spontaneous decay of the upper level.
is rate of the spontaneous decay of the upper level.
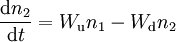 ,
,
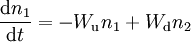
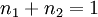 .
.
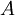 at the pump frequency and
the gain
at the pump frequency and
the gain 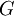 at the signal frequency can be written
as follows:
at the signal frequency can be written
as follows:
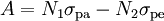 ,
,
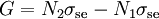 .
.
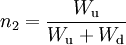
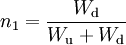
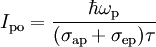 ,
,
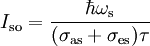 .
_
The absorption at strong signal
.
_
The absorption at strong signal
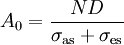 .
.
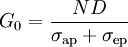 ,
,
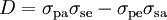 is determinant of cross-section. For the efficient gain medium, this determinant should be pretty positive.
is determinant of cross-section. For the efficient gain medium, this determinant should be pretty positive.
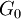 , and absorption never exceeds value
, and absorption never exceeds value 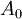 .
.
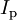 ,
, 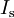 of pump and sigmal, the gain and absorption
can be expressed as follows:
of pump and sigmal, the gain and absorption
can be expressed as follows:
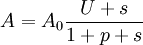 ,
,
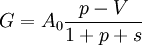 ,
,
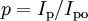 ,
,
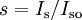
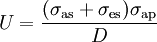
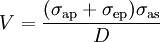
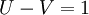 ,
,
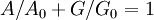 .
.
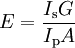 .
.
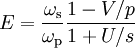 .
.
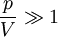 , and
, and 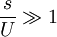 .
.


